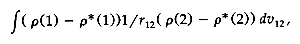Hall, 2000 |
 |
This text originates from:
International Journal of Quantum Chemistry, 74, 439—453 (1999)
© 1999 John Wiley & Sons, Inc.
Recollections and Reflections
George G. Hall
Shell Centre, School of Education,
University of Nottingham,
Nottingham, NG7 2RD United Kingdom
Received 25 November 1998; accepted 16 February 1999
Note: This work is dedicated to Doreen, my wife,
whose love and care have always inspired and supported me.
Career Venues
EARLY DAYS (1925-1943)
Most of my primary schooling was in Mountpottinger
Public Elementary School, in the east
side of Belfast, a school now closed. It had a high
reputation for copperplate writing and a very strict
discipline. While affected permanently by both of
these, my most exciting memory of this period
was our introduction to Euclid whose first
propositions we had to learn by rote.
From there I went to Regent House School, in
Newtownards. There I came under the influence of
many good teachers and found myself attracted to
mathematics and science, though I was also
learning both Latin and Greek. I then had one year in
Methodist College, Belfast, to prepare for the
entrance scholarships to Queen’s University.
QUEEN’S UNIVERSITY, BELFAST (1943—1947)
When I entered Queen’s University in 1943, I
realized quickly that science was the kind of career
I most wanted. The war was still dominating
everything, so career planning was in obeyance.
Northern Ireland had no conscription, but I joined
the Home Guard at a time when an invasion
seemed likely. During the undergraduate course, I
became increasingly attracted by Prof. P. P. Ewald.
He was a good lecturer, not an orator but a
stimulating and perceptive innovator. His philosophy of
bringing together mathematical techniques and
physical situations in order to bring insight into
both has deeply influenced me. I also owe much to
Prof. K. G. Emeléus, in Physics, and to Prof. H. R.
Pitt and Dr. Mostyn, in Mathematics. I graduated,
B. Sc., in 1946 with Firsts in both pure mathematics
and mathematical physics.
I had begun to read Dirac’s Quantum Mechanics,
stimulated by physics lectures on atomic spectra
and mathematics courses on Hilbert spaces, but
had no proper exposure to quantum mechanics so
I remained for another year to complete the degree
course in experimental physics, from which I
gained another First in 1947. During this year I
also started research, with my good friend Herby
Deas, on a little investigation suggested by Ewald
into the vibrational spectra of coronene. This
involved us in learning group representation theory
and applying it to the problem. I have remained
interested in group theory as a beautiful and
useful technique ever since. This interest in coronene
was mentioned when I applied to Cambridge to
become a research student and was the reason I
was assigned Prof. Lennard-Jones as my
supervisor. From such small beginnings was I pointed to
quantum chemistry.
CAMBRIDGE (1947-1955)
In 1947, Cambridge was just beginning to
recover from the effects of the war. Sir John
Lennard-Jones had had a distinguished war career
in the Ministry of Supply. I and two other
Cambridge students, were his first group of research
students on his return. He was anxious to revive
his interest in quantum chemistry [173] and move
on from the statistical mechanics of liquids, the
topic which had dominated his immediate prewar
research. He decided to formulate molecular
orbital theory rigorously and began by deriving the
differential equations for the best orbitals. I found
this approach very attractive because the
contemporary theories of the subject seemed to me most
vague and unsatisfactory in their foundations.
After three years, in 1950, I had the good
fortune to be appointed to the post of Assistant in
Research in Theoretical Chemistry. This gave me
my first experience of university lecturing. Then,
in 1953, I succeeded in the competition, open to all
young graduates in the university, to be elected to
a fellowship in my own college of St. John’s.
About this time, the university was building its
first electronic computer, the EDSAC. Frank Boys,
who had joined the Theoretical Chemistry
Department in 1948, was one of the very first to use it,
and his work on molecules would have been
impossible without it [175]. I attended the first M.Sc.
course on programming and was soon writing my
own suite of programs.
On reflection, I can see that the topics on which
I started work in Cambridge have remained with
me all my life and have surfaced again from time
to time as relevant new ideas matured and
developed. I still try to introduce new mathematical
ideas into the subject. I have continued to use
group theory. I have learned much from
developments in solid-state physics. Conjugated
hydrocarbons haunt me! The biological applications of our
work remain a vital, if often distant, goal.
Nevertheless, I have a marked tendency to pursue any
side issues that present themselves attractively to
me. This has led me into many interesting
investigations at the cost of a certain incoherence. The
many not-otherwise-cited articles in the
publication list give proof of this.
LONDON (1955-1962)
My interest in solids led to the offer of a
Lecturership in Mathematics in Imperial College, where
the solid-state group was flourishing under Prof.
H. Jones, E. P. Wolfarth, and others. Because it
covers such a wide area, London is a very different
university from Cambridge and personal
relationships are much harder to develop. Although I
enjoyed being part of the solid-state group, I did
not feel sufficiently attracted to switch my research
entirely to that area.
In 1957, I received an invitation from Per-Olov
Löwdin to spend a year in Uppsala, Sweden, and
the department gave me permission to accept. On
my return to London, I was given the chance to set
up my own research group. Initially, Terry Amos
joined me and later Don Rees and Arturo
Hardisson. We had to take time learning how to exploit
the new computer of London University.
SWEDEN (1957—1958)
The invitation from Per Löwdin to spend a year
in Uppsala came at a good time for me. It gave me
the opportunity to think over my future plans and
to decide how to proceed. It was also a chance to
learn fully the ideas and approach of that group. In
the group’s determination to be rigorous and
innovative, its members were close to my goals, but
there were some important differences, such as my
continued interest in semi-empirical theories as the
best bridge between the then unattainable accurate
solutions and the ad hoc regularities often found
during the analysis of experimental results.
An important event during this year was the
summer school held in Vålådalen, in the north of
Sweden. This was the first of these events and set
the pattern for many since then. We had many
lectures and talks and, during the final week, a
number of very distinguished visitors joined us to
discuss and debate aspects of the subject [21]. I can
remember illuminating sessions with Mulliken and
Pauling, as well as with Löwdin, Preuss, Jensen,
McWeeny, Matsen, Pauncz, and Shull, and several
eminent experimentalists. It was a good
illustration of the friendly nature of our colleagues and of
the real interaction between ideas that they
encouraged. One outcome for me was the letter [22]
that Harry Shull and I wrote asking for specific
names to be given to the atomic units of energy
and length and urging that these should be the
hartree and the bohr.
NOTTINGHAM (1962-1983; 1988- )
My appointment to the chair of Applied
Mathematics in Nottingham, in 1962, opened up a new
range of possibilities both for me and for the
university. Nottingham had just split off a
Theoretical Mechanics Department from its Mathematics
Department to take over the teaching of
mathematics to engineers, and this department had
major research interests in classical mechanics so that
the Mathematics Department could allow its
applied section to concentrate on quantum theory.
This came at a time when university expansion
was taking place, so that new staff were being
appointed each year and their specialisms could be
determined. The Mathematics Department became
and remains one whose applied section is
predominately concerned with quantum theory.
I brought with me my Imperial College group,
and Raphy Levine joined us as a research student.
We had the disadvantage that, at that time,
Nottingham had no computer so our work became
theoretical rather than computational.
In 1970, we held a Quantum Theory Conference
in Nottingham. It was designed, in particular, to
help young researchers. At its conclusion, it was
decided to continue the event, and Coulson and I
offered to host the meeting each year in turn. The
series continued until recently but, sad to say, has
now come to a halt.
It was a great encouragement to me to be
elected, in 1974, to the International Academy of
Quantum Molecular Science. I also appreciated
being elected to serve, from 1977 to 1980, on the
Executive Committee of the International Society
for Quantum Biology.
Inevitably, I was drawn into university
administration and, from 1972 to 1975, I served as Dean
of Pure Science. This took considerable time away
from research. I represented the university on the
Derbyshire Education Committee from 1966 to
1974. I also served on three national committees,
on the Computer Consultative Committee of the
Department of Education and Science (1972—1976),
as Chairman of the Joint Mathematical Council
(1979—1981), and on the Mathematics Committee
of the Council for National Academic Awards
(1980—1983). The validation activity of the latter
led to my first visit to Hong Kong in 1982.
From my first term in Nottingham, I have been
involved with mathematical education in the
schools. The department, then, ran courses for
teachers in the "new math," which was being
developed and introduced into the school
curricula. Professor Halberstam (my pure mathematics
colleague) and I thought through our contribution
to this work and decided, eventually, that we
should concentrate on in-service courses rather
than formal vacation courses. For this purpose we
lobbied our then vice chancellor, the late Lord
Dainton, for support, and he assisted with the
negotiations to obtain finance from the Shell
Company, in 1967, to enable us to appoint several staff
members to help us in this work. The Shell Centre
has continued its mathematical education work
ever since. The Shell finance has now finished but
contracts from other sources, many of them
overseas, support research and the dissemination of
"best practice" worldwide. The Shell Centre aims
to digest the best of the current research on
mathematical education and make it available to
teachers. It designs teaching material, which is carefully
tested in schools, to ensure that it is robust enough
to be used by the average teacher. More recently, it
is working on ideas of balanced assessment and on
the theory of how to disseminate good practice.
In 1982, the universities in England first came
under severe external pressure to cut staff. My
department was threatened with the loss of several
people because the staffing formula said we were
over staffed. After much thought, I decided to take
early retirement and avoid having to select others
for removal. The arrangement allowed me to
remain, under reduced teaching load, for one year. I
became an Emeritus Professor and as such still
retain a few rights in the university.
KANSAS (1969—1980)
One visitor to our group, as a post-doc for a
year, was Ralph Christoffersen [44]. He, then, took
up a professorship in the Chemistry Department of
Kansas University at Lawrence. A little later, in
1969, I received an invitation to spend a semester
there with his group. I found this a very
stimulating experience, partly because of his activity and
partly because the department proved to be a
friendly, helpful place with an orientation toward
both teaching and research. I delivered an
advanced course for research students describing and
commenting on the principal methods then in use
in our field. I had hopes of publishing this, but the
result was, inevitably, very similar to the book of
McWeeny and Sutcliffe, which appeared about that
time, so I abandoned the manuscript. The
consequence of my visit was that it was arranged that I
would return for a month or two each year,
perhaps to teach a course but always to coordinate
our research. We kept up this Kansas connection
for 11 years despite problems in financing the
travel and subsistence. The contact continued until
Christoffersen left Kansas University.
KYOTO (1983-1988)
During my transition year in 1982, I received
several overseas job offers, but the one that
interested me most was from Kyoto University. They
were setting up a new department devoted to
molecular engineering and wanted me to head the
quantum molecular science section. This was an
exciting opportunity to be in at the start of
something new as well as an opportunity to experience
a different civilization and culture. I accepted the
post and then, almost immediately, experienced
the impact of red tape, which seems to be an
essential part of any Japanese official activity [171].
I am grateful to my Japanese colleagues for their
help through this difficulty.
My time in Kyoto was the most productive time
of my life, both as regards producing research and
as regards my learning about Japan. Since Kyoto is
the former capital, it retains many traces of its past
and has been allowed to preserve them. My
colleagues helped me to experience the depth of
Japanese thinking and feeling. I tried to reciprocate
by helping them toward a more idiomatic use of
English [170]. I was helped by many good research
students whose commitment to the work was
often remarkable [165].
I was greatly moved to receive from Kyoto
University, in 1989, their first honorary degree of
D. Eng.
MUNICH (1992, 1993)
I have enjoyed two periods of work with Gerd
Diercksen in Munich. His programming project is
an ambitious one that aims to provide a complete
molecular calculation package, OpenMol, which is
user-friendly and capable of accepting many
add-ons. It uses object-oriented programs and has a
expert program embodied to guide the user
through its options. We collaborated to write a
semitechnical account of it [131].
Research Themes
LOCALIZED EQUIVALENT ORBITALS
An immediate consequence of the Lennard-Jones
formulation of molecular orbital theory was his
realization that the orbitals, when doubly
occupied, could be transformed by a unitary
transformation without any change of wave function. As
John Pople and I worked through the implications
of this, we realized that the chemical consequences
were very important. For the first time, we had a
rigorous definition of a chemical bond as a
localized equivalent orbital [3] and could develop its
properties. The term "equivalent" combined the
ideas that these were unitary transforms of the
canonical molecular orbitals and that, when
symmetry was present, they could be generated from
one another by a permutation. I took special
pleasure in introducing [2] the idea of a permutation
representation of a group into the subject.
"Localized" meant that the total self-energy of the
orbitals was a maximum [20]. Because it is
independent of basis set, this definition of a bond is still
correct. It enables the chemist to know where each
electron is and what it is doing. The extra terms,
added to the wave function in order to achieve
high accuracy, can be described as adding
correlation inside each of the localized orbitals and
between them. The advantage of localization is that
the bonds become more nearly determined by their
terminal atoms alone and their energies should
then become constant. Since the major error in the
theory is its neglect of electron correlation within
the localized orbitals, there is reasonable ground
for believing that the corrected bond energies.
would also be constant.
Some time later, Jane Hylton and I carried out a
regression analysis of the Hartree—Fock energies of
a long series of molecules [73] and showed that
they could be turned into a simple additive set of
atomic and bond energies. This is positive
evidence in favor of our ideas of bonds in molecules.
These bond energies even showed the effect of
eLectronegativity. From the results of calculation
we could recover concepts of chemical importance.
Unfortunately, in 1950, there was no hope of
solving the molecular orbital differential equations
so our discussions about the orbital structure of
molecules, except in as far as group theory
determined them, were rather approximate. I tried to
remedy this by projecting the molecular orbital
equations into a finite-dimensional function space
[4] and so derived the matrix equations from which
approximate orbitals could be found
systematically. This theory ran into controversy
immediately because it contradicted the accepted theory at
that time, which assumed linear orbital equations,
whereas the proper equations were cubic [121]. I
was warned to publish with care and to avoid
trouble!
Using ideas from alternant matrix theory, Terry
Amos and I later developed [28] the idea of
corresponding orbitals, first suggested by Löwdin, for
treating unpaired systems, using unrestricted
molecular orbital theory, and calculated some
examples. Since these wave functions were not
eigenfunctions of spin and since eigenfunctions of
spin were too complicated for our computer, we
had to introduce a compromise wave function in
which, by applying an annihilator, the worst of the
spin contamination was removed.
IONIZATION POTENTIALS
My most interesting achievement in Cambridge
was my semiempirical theory of ionization
potentials. This was a correctly defined theory [4, 7, 8]
but, simply because we could not then calculate
them accurately, its defining integrals over
equivalent orbitals became parameters to be determined
from experiment. It assumed that Koopmans’
theorem was exact and, although this is not strictly
true, it is a reasonable approximation because its
errors are in opposite directions and so tend to
cancel. At the time, accurate experimental
ionization potentials were becoming available so the
theory had a good interaction with experiment and
helped to identify the ionic states involved. It was
very successful for a certain class of molecule [11,
13] but failed for others.
Later work [56], with Keith Gregson, proved
that this failure was due to the neglect of the
strong intramolecular electric fields within some
ions. When these are included, along with the
internal polarization, which is a part of the
correlation energy, the agreement with experiment is
again impressive. Classical ideas of the electric
field and its effects on charge clouds are still
sufficient for this purpose. I learned from this the
lesson that the electrons in a neutral molecule can
be described as localized and are polarized by any
electric field they may experience, but that, on
ionization, one electron is no longer paired and is
subject to quantum delocalization.
I realized in 1970 [58] that the ideal tool for the
discussion of ionization potentials was the
one-electron Green’s function, but it was not until 1988
that a student of mine, Y. Mizukami, actually did
such a calculation [112].
HÜCKEL THEORY AND GRAPH THEORY
I adapted my semi-empirical theory of
saturated molecules to conjugated hydrocarbons [5, 6]
by introducing what I called the "standard excited
state." In this state all the pi electrons are given the
same spin and so require twice as many orbitals.
These orbitals can be localized and give one pi
function for each conjugating atom. For the ground
state, the most stable set of molecular orbitals are
then doubly occupied. There is an implicit appeal
to the Koopmans result that orbitals are little
changed, whether singly or doubly occupied. This
procedure enabled me to justify much of what was
called Hückel theory in rigorous terms, showing
[14] that it approximated closely to the ab initio
calculations available at that time. In particular,
the pi functions were well localized, and their
various two-electron integrals were negligible
except for the classical Coulombic terms. The theory
did point, however, to the presence of several
extra nonlinear terms in the total energy.
Unfortunately, my standard excited state offended
conventional tastes and has been largely ignored despite
its logical and computational success.
I defined alternant matrices in general [16],
using partitioning, as those with the form
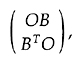
where 0 is a zero matrix and B may be
rectangular, and derived the properties of their
eigenvectors and eigenvalues. In effect, the matrix B is
diagonalized by two unitary matrices.
This result allowed me to give a closed form
[16] for the bond orders of alternant hydrocarbons
in Hückel theory. In another work [18], I showed
how the molecular orbital equations could be
solved in a computer and, as a demonstration,
listed the bond orders for 25 aromatic
hydrocarbons. Since bond orders for hydrocarbons were
then the most successful part of molecular orbital
theory, because they correlated very well with
crystallographic results on molecular dimensions,
these were a source of theoretical information for
experimentalists. They also gave us important
guidance about the relations between molecular
shape and molecular properties. The idea of
embedding a molecular fragment within a molecule
as a means of predicting the degeneracy of certain
molecular eigenvalues is one example of these
relations. In particular, the calculations on
benzpyrene, a potent carcinogen, showed that it had
an unusually large bond order in what the
Pullmans called its K region. The study also included
the results of a self-consistent calculation, which
included the extra nonlinear terms given by the
theory. The calculation was very similar to those
performed under what was later known as PPP
(Pariser, Parr, Pople) theory.
The structure and interactions of the
tricycloquinazulenes was another topic of biological
importance that we considered, later, using this
pi-electron formalism [59, 74]. These molecules have
some N atoms in their hexagonal rings and include
some of the most potent carcinogens known. Our
pharmacists were anxious to have information
about them and their activity. William Rodwell
and I produced approximate electronic structures
for these molecules and examined their
interactions with other species. The conclusion was
reached, on energy grounds, that an intercalation
of these into a DNA chain was possible and could
account for their cancerous interruption of
biological function.
In Kyoto, I started to investigate conjugated
hydrocarbons large enough to have a hole
surrounded by hexagon rings [110]. This requires the
introduction of the idea of the genus of a molecule
- the number of its holes. In this connection, I
introduced the concept of the bual [154] of a graph,
which is a modified form of its graphical dual. By
repeatedly taking the bual, a graph can be stripped
down, from the outside, in onion fashion. These
molecules are now called coronoids and have been
well-studied. I also looked [114] at the connection
with the superdelocalizability, an index measuring
molecular reactivity.
Another investigation begun in Kyoto was into
the forms, in Hückel theory, for the energy of
infinite periodic molecular systems. My student, S.
Arimoto, proved that the total energy tends to a
linear function of the number of repeating units
and that we could calculate the leading term in
this asymptotic expansion using an integral [123].
We then deduced a number of exact asymptotic
expansions of this energy for different series of
molecules [130]. The same argument applies to the
total zero-point energy of periodic molecular
systems and, with some changes, to the heats of
formation of polymers and solids.
On my return to Nottingham, I took up again
my continuing problem about the total pi energy
in what is now called the graph theory of
conjugated hydrocarbons. My empirical expression for
this [89], given years before in 1981, was based on
an analysis of many actual calculations and had
the form
E = 0.442n + 0.788N + 0.34K(0.632)N-n,
where n is the number of C atoms, N the number
of CC links, and K the algebraic number of Kekulé
structures. This can be backed up with some
theory [103, 120, 122, 127], using the moments of
eigenvalues to define other graphical invariants
and expressing the energy in terms of these, but
this fails to explain the third term in the equation.
Although, working with Ivan Gutman [124, 125,
132] and considering the eigenvalue spectral
densities, we have made some progress in
understanding this problem and showing the limitations of
this expression, it remains a tantalizing result.
Nowadays, this treatment of hydrocarbons is
important both as a means of understanding this
rich class of molecules and also as a respected
branch of graph theory. Its relationship to
molecular orbital or PPP theory tends to be ignored.
SOLID STATE
As an offshoot of my interest in localized
equivalent orbitals, I first became interested in the band
theory of solids and in diamond in particular [9,
10, 12]. The interaction of bonds in a hydrocarbon
and in a solid have much in common. Treating the
solid as a set of localized orbitals, which have a
strong local interaction but a negligible more
distant interaction, leads immediately to an explicit
form for the energies of the various bands [19] and
the parameters in this, which measure these
interactions, can be fitted well using other calculations
of the bands.
While in Sweden, I developed [33] a
semiclassical version of the theory of excitation waves in a
molecular crystal. This showed that, in the crystal,
the transition dipoles of different molecules
interact in the same long-range way as do the
molecular dipoles and must be treated with equal respect.
During a short visit which he paid to the
division in Kyoto, I worked with Tom Claxton on the
spin density at the nucleus of trapped muonium in
a solid using various simple models of the solid
[107]. Later, with my student Y. Mizukami, we
took up the problem of muonium trapped at a
specific site in diamond using a realistic form for
the electrostatic potential acting on the muonium
and obtained a reasonable agreement with
experiment [108].
OPIT COMPUTER PROGRAM
With the development of computing center
facilities in Nottingham our group took on, in 1969,
a programming project to produce a package,
called OPIT, which used optimized floating
spherical Gaussians (FSGO) in a molecular orbital
calculation [63]. This used ALGOL and so made
extensive use of procedures. In effect, it was an early.
form of object-oriented programming. Many
people contributed to this project. We had support
from Prof. G. Cook at Leeds and Prof. R. A. Sack at
Manchester. Among those who spent many hours
on it here were Drs. Brailsford, Packer, Ford,
Hylton, Schnuelle, and Tait. The purpose was to model
molecular calculations by using a small set of
spherical Gaussians, well optimized in position
and scale. This could not claim high accuracy but
it could, and often did, mimic what much more
elaborate calculations were doing. As such, it
served a didactic purpose [64, 72]. It allowed us to
discuss molecular shapes, dipole moments and
even some excited states. We had hopes that we
could find a reliable correlation between its results
and those of more accurate calculations.
Some of our learning was unfortunate. By
having exclusive use of the local computer for a brief
period, we showed that it had an erratic least
significant bit in its arithmetic unit which
prevented its results from being exactly reproducible.
We also learned that a strict optimization tests
many aspects of a program and often highlights
minor weaknesses in the numerical analysis. The
sad consequence was that many of our results
were not fit to publish. This was an important
experiment and taught us much, even though,
eventually, it became clear that our hypothesis,
that we could simply scale up our energies to
reproduce the accurate results, although broadly
correct, was not sufficiently accurate to be useful.
One of the important and successful
investigations, made at this time using OPIT, was into the
structure of phenethylamine and amphetamine.
Colin Miller, Gary Schnuelle, and I showed [76]
that these, when neutral molecules, preferred an
extended configuration but that their protonated
forms had the side chain folded over the benzene
ring. This folding helps to protect the charge
during the motion of the molecule through the liquid
and so could have important implications for the
biological action of these molecules as
neurotransmitters. We also used point-charge models of
water to investigate the shifts of their spectra in
solution [82].
PERTURBATION THEORY
My first study [1], in 1950, used perturbation
theory to investigate the accuracy of Koopmans’
theorem and showed that a molecular orbital
changed very little whether it was doubly or singly
occupied. We have been using forms of
perturbation theory ever since. In London, Arturo
Hardisson and I performed various computer exercises
on the implementation of self-consistent molecular
orbital theory including applications to ring
currents, chemical shifts, and g factors [32, 36, 37].
These were the first practical applications of
coupled sell-consistent pertutbation theory. The
results were of immediate interest to the
experimentalists, specially L. M. Jackman, with whom we
collaborated [30, 34]. In Nottingham, Terry Amos
and I again employed coupled self-consistent
perturbation theory within the PPP context. The
theory of electrical polarizabiity of conjugated
hydrocarbons [46, 47], which we developed, is one
example.
I found the theory of the transcorrelated wave
function, by Boys and Handy in 1969, an attractive
challenge to mathematical principles [57]. With
Edward Armour, I tried to explain some of its
success by investigating nonsymmetric
Hamiltonians. This gave some insight but failed to show
how the theory could be put on a firmer
foundation. I later developed an infinite-order
perturbation theory [83]. By writing the perturbed wave
function in the product form i/i = ekfr, where ~ is
the unperturbed wave function and L is a function
of position, we obtain the equation for L which has
the form of a first-order perturbation equation:
(HL - LH) φ = [HL] φ = (W- V) φ.
If necessary, this can be solved using a variational
principle. The perturbing potential V includes a
nonlinear feedback term:
V = H - H0 + 1/2 [[HL]L].
Because of the change in the V potential, the
equations are nonlinear and must be solved
self-consistently. This formalism is powerful enough to
deal successfully with some notorious examples
where the conventional theory fails. I related this
theory to the transcorrelated theory and showed
how this form of perturbation theory leads to all
the equations and the major ideas of the theory
[80]. Cohn Miller and I applied the ideas to the He
atom with a simple correlated wave function [85]
and showed that these equations did agree
substantially with the Boys-Handy ones and led to a
good solution.
The form of this perturbed wave function as a
product shows up the limitation of this theory.
Since eL is always positive, no function L can
change, for example, the nodes of φ so the
perturbation cannot correct such features in the φ
function. For a more flexible perturbation theory, L
must become an operator. This leads naturally to
the cluster wave functions.
SOLVATION
Ralph Christoffersen, in Kansas, was intent on
using Gaussian models to investigate
biological-sized molecules and to probe typical biological
behavior such as photosynthesis and electron
transport. Since these did not usually require great
accuracy but did need to show the various
possible phenomena, it required a different attitude to
molecular calculation [71]. We collaborated in
devising methods of including solvation effects and
began to develop two approaches to this. One of
these was based on a more accurate treatment of
the electrostatic field effects inside a cavity large
enough to contain a molecule [70, 78]. The other
used point-charge models to evaluate the
molecular electrostatic potentials acting on a molecule
arising from its neighboring molecules [79]. In
some examples we combined the two and
represented the hydrogen-bonded waters as sets of point
charges surrounding a solvated molecule and then
set the combination in a large spherical cavity.
Cohn Smith and I, in Kyoto, took a more radical
approach to the subject. We considered [115] a
model of the molecular surface and found the
averages of the molecule’s electrostatic potential
and electric field over the surface around each
atom. These give measures of the molecule’s
interaction with the surrounding solvent molecules.
They should also be used in discussions of
molecular recognition. With such quantities we showed
that the solubility of many molecules could be
satisfactorily predicted. In the course of this we
applied fractal theory to show that the volume and
surface area of a molecule in solution are not fixed
but depend on the size of the liquid molecules.
REACTION SURFACES
Since I was lecturing in Kyoto on reaction paths,
I tried to extend my research [93] in this direction
I produced [95] a model reaction surface for
hydrogen transfer reactions which assumed three
atoms, with internuclear distances x and y,
reacting in a straight line. The potential is based on the
Morse potential and has the form
V = A ( X 2 - 2X ) + B ( Y 2 - 2Y ) - 2HXY,
where X = e — ax , y = e — by , and A, B, a, b are
known from vibrational data on the diatomic
molecules. The parameter H is not known in this
way, but I proposed that it should be given by the
formula
H = ( A 5 - B 5 / ( A 4 - B 4 ).
This form leads to a good correlation with reaction
barrier heights and gives a good account of the
reaction geometry and the qualitative aspects of
these reactions.
Mayumi Okada and I tried [96, 97] to extend
this more generally using sums of higher powers
of X and Y as potentials. These solve the
asymptotic problems of representing reaction surfaces
but, because of differencing, are found to be too
sensitive to be used freely.
The problem, highlighted by R. C. Woolley, that
"all isomers satisfy the same Schrödinger
equation", is another major unsolved problem for our
subject. During the course of our work on
potential surfaces, the advantages of using diabatic
reaction surfaces rather then adiabatic ones became
apparent [97]. These allow the global symmetry to
be broken in defining the species but restored later
at the point where the surfaces intersect and the
distinct species interconvert. A similar method of
breaking symmetry should contribute to the
solution of the major problem. I suggested [105] that,
when the isomers can be defined as permutations
of one another, and the Schrödinger equation is
solved with a permutation constraint, the resulting
diabatic surfaces would give an approach to this
problem.
POINT CHARGES
I first became interested in point charges when,
as an undergraduate, I studied the calculation of
the capacity in classical electrostatics. I was
minded of this when I realized that the electro
restatic potential of a Gaussian distribution of charge
is asymptotically that of a point charge and, then,
that the product of two Gaussians at different
points is another Gaussian at a point on the line
between them. Thus a wave function, whose
electron density p is a quadratic form of spherical
Gaussians, can have its p immediately translated
into a point-charge model [67]. Since our FSGO
calculations using OPIT were of this type, we
could investigate the consequences. Andrew Tait
and I found [68] that the molecular electrostatic
potential was evaluated very well outside the
molecule itself using the point charges, though
there were a large number of these. The model
conserved the total charge and dipole. David
Martin and I [87, 88] strengthened this result by
proving the theorem that, if the electron density p is a
sum of Gaussians, then a good point-charge model
is obtained by retaining their charge but shrinking
each Gaussian into a point charge. Thus, if
M( x, y, z) is a harmonic property (i.e., V2M = 0)
to be evaluated, its value is given exactly by the
sum over point-charge contributions:
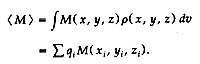
We also extended the theory to’allow nonspherical
Gaussians to be included, but the results became
less convenient.
When I looked at some of these models of
atomic densities in molecules with K. Tsujinaga,
we realized [101] that it was important that each of
the heavy atoms should have one diffuse Gaussian
to represent its outer charge density. Then, when
the remaining Gaussians are shrunk to points, this
function remains to model the more sensitive outer
density. When the molecule is placed in an electric
field, this function is moved and so contributes the
major part of the molecular polarization [102].
Because of this, the diffuse function also models the
dispersion forces between molecules in a practical
way. It can also model the surface shape of the
molecule and allow for penetration effects [31].
The name, the “current bun” model of an atom in
a molecule, in which positive and negative point
charges are embedded in a diffuse negative cloud,
does homage to the ideas of Lord Kelvin and J. I.
Thompson on atomic structure.
ATOMIC CHARGES
A typical wave function, nowadays, is too
complicated an object to understand and, often, it is
too elaborate even to extract from its home in a
computer. Fortunately, however, we know from
density functional theory that all the important
physical information is contained in the electron
density, so this has to be our object for study. The
distillation of useful information from the
available oversupply is an important problem in this
computer age, so we have a chance to study the
electron density as an example of this. In more
abstract terms, we need to produce a higher level
concept from lower level ones, scientific synthesis
rather than analysis.
Having surveyed thç alternative definitions on
offer [94], I decided that we should consider a new
starting point. Cohn Smith and I began [92, 98, 99]
by using our FSGO experience as a guide. We
approximated the density, p. of a conventional
molecular orbital calculation by p~, a linear sum
of spherical Gaussians. The positions and scales of
the Gaussians could be optimized. We needed a
criterion for the fitting, so I suggested [90] that the
error self-energy,
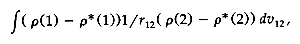
should be minimized. This is based on the familiar
Dirichlet principle in electrostatics and can be
further justified using the theory of splines.
Alternatively expressed, it is a least-squares fit of the
electric fields produced by the two densities.
Using this criterion, Tsujinaga and I
investigated [101] the approximation of a given
molecular charge density by spherical Gaussians placed in
optimum positions and with optimum charges. We
found it helpful to add the constraint of fixing the
total charge. Our studies showed that it was
important to balance the number of Gaussians
associated with each nucleus to obtain the best fits.
Where lone pairs were present, a Gaussian at their
center represented them and improved the fit. The
results tended to converge after a modest number
of terms. The resulting charges could, therefore, be
defended as physically rather than mathematically
based.
Although the Gaussian is well-adapted to locate
the charges, within a molecule, it is somewhat
artificial. This led Smith and me to introduce [104]
the "optimal population analysis." In this, the
approximate density is represented as a sum over the
squares of the atomic orbitals already in the
density matrix. The optimization is limited to the
linear coefficients of these squares. This gives a
procedure only a little more complicated than the
Mulliken populations but much more clearly
based. We showed its realistic advantages by
evaluating the different contributions to the total
molecular energy using this density. The result
was a considerable improvement over the
corresponding Mulliken estimates. We found, however,
that the results were not independent of
hybridization and that localized atomic hybrids gave an
even better representation of the density and of the
energies. Atomic hybrids allow us to give a more
detailed description of the location of the charges
but force us to allow charges not to be on nuclei.
Chemically speaking, atoms are not spherical and
can have dipoles as well as charges. By using very
localized functions, we can turn most of the energy
contributions into classical electrostatic energies.
One consequence is that the exchange and
correlation energies then become very small. When the
theory can describe where the electrons are
localized and show that almost all the molecular
potential energy is then electrostatic [118], an
understandable account of a molecule becomes possible.
The goal of an agreed definition of atomic
charge, which is independent of the basis set being
used and which facilitates a physically meaningful
analysis of the forces within a molecule, has yet to
be reached. Nevertheless, its shape is slowly
becoming more clear. Optimization will lead to more
stable estimates and a better understanding of
localization will lead to energy contributions that
explain the structure and properties of the
molecule.
LOCALIZATION
Recently, I have begun to work again with Don
Rees. We started by thinking about atomic hybrids
[133—139]. The operators x, y, and z clearly
commute but, when we take their matrix
representatives in a finite-dimensional function space, these,
in general, do not commute. One modification
which often produces commutation involves a
scaling of some of the basis functions [136]. In
other examples [134], we must add extra operators
to compensate for the finite dimensions. The atomic
hybrids are the simultaneous eigerifunctions of
these commuting matrices. These hybrids are the
most localized functions according to the
definition given by Boys. Their use in describing the
structure of a molecule and evaluating its energy
contributions will be a contribution to our
understanding of molecules.
Our work, which is now progressing actively
[141—143], can also be described as the
generalization of Gaussian quadrature to higher dimensions
since the Gaussian grid points are at the centers of
the hybrids and their weights can be derived from
the value of the hybrid at its center. It is an
important property of these hybrids that each has
nodes at all the other grid points. The systematic
use of Gaussian quadrature in molecular
calculations, which we hope to encourage, would give a
greatly increased flexibility in the choice of basis
functions. It would also eliminate many of the
integral complexities from programs.
In its quadrature form, our theory can be
generalized to solid-state calculations by using cosines
as the basis functions rather than polynomials [140].
The resulting grid points are the "special points"
used extensively in solid-state calculations of
integrals over reciprocal space.
MATHEMATICAL IDEAS
During my stay in Sweden, I showed how to
make the radial variable a function of another
auxiliary variable and so produced a
two-parameter orbital function for the helium isoelectronic
series which reproduced the Hartree—Fock results
[23].
I was specially pleased to prove [25] that, for
such isoelectronic ions, the electron-nuclear
potential energy can be defined as Z a W/dZ, where
W(Z) is the energy as a function of nuclear charge
Z. Chemistry may be confined to integral values of
Z but mathematics is not. Don Rees and I later
used this expression [29] in our calculation of
magnetic shielding constants for atoms.
While he was with us, Raphy Levine used
operators extensively in his work on time-dependent
properties, and we learned from his example [45].
In particular, the use of Green’s operators and
functions was a natural development of working
in the town where Green had lived [176]. I
proposed a variational principle for the energy [50, 55]
using a Green’s function and proved that it always
gave better energies than the Ritz—Rayleigh ones.
As Don Rees, John Hyslop, and I discovered [54, 60],
its use for problems with more than one
electron proved difficult.
One of my colleagues in Nottingham was
Kathleen Collard, and we become interested in the
application of differential topology to analyze the
shapes of the electron densities of molecules. We
suggested [84] the use of orthogonal trajectories to
define the bonds between nuclei. We could also
relate the numbers of turning points of different
kinds in the density by using the Poincaré-Hopf
theorem. We looked carefully at possible
catastrophe points. I later [100] extended these ideas to the
molecular electrostatic potential.
H. Nobutoki and I tried [113] to understand the
pattern of vibrational energy loss associated with
the dephasing that occurs at the start of an
electronic transition. We calculated many examples of
the time evolution of the water molecule from
various initial vibrational states and tried to find
the common pattern. With a little help from
information theory, we could rationalize some of the
observations but a good theory eluded us.
N. Saito and I [117] looked at the effect on a
molecule of embedding it in an intense laser field.
This became an interesting exercise in radiation
theory but seemed to be of small chemical impor-
tance since the only significant effects were for
hydrogen atoms.
MATHEMATICAL EDUCATION
I have tried to contribute to the work of the
Shell Centre through some research as well as in
various other ways. One research piece which
influenced me considerably [161] was an
investigation into the motivation of mathematics students.
This showed conclusively that their university
experience was killing their strong initial
mathematical motivation quite rapidly. I then tried to reverse
this by redesigning courses in our degree program
[149, 162] so that they concentrated on tackling
realistic practical problems by model-building, but
the initial improvements were not sustained and
did not convince my colleagues.
I also support the aims of the Shell Centre by
producing small examples of original applications
[177—206], principally for the Bulletin of the
Institute of Mathematics and its Applications, now called
Mathematics Today. These follow a common pattern
which I have developed. Each must arise from
some everyday observation or reflection. Each must
have one basic mathematical point to make. The
length should not exceed one page in print and is
often about half a page. I see these almost as a new
art form!
To look back is to look forward. It is rarely
possible to look at scientific work and know that
the last word on it has been spoken. When I look
at all the topics on which I have worked, I see so
much that still needs to be done both to extend the
theory and to produce examples which publicize it
and prove its worth. While I have every intention
to continue working on many of these, I can offer
no guarantee that I will not be deflected into some
entirely different direction!
G.G. Hall's Books
MATRICES AND TENSORS,
PERGAMON, 1963
While in London I started to write a book on
matrices and tensors. The book was intended for
chemists beginning our subject. It combined two
aims. The first was to explain, as simply as
possible, how practical calculations on matrices can be
performed by hand or on a computer. The second
was an attempt to explain how tensor ideas
provide justification for the "vector model" used in
angular momentum theory. The book, which is a
volume in the International Encyclopedia of Physical
Chemistry and Chemical Physics, did not try to cover
all aspects of the topics. it is still used but no
longer sold!
APPLIED GROUP THEORY, LONGMAN, 1965
This is a graduate textbook. I had become
dissatisfied with all the current texts on group theory.
They seemed to me overelaborate and not
compatible with the ideas of quantum theory. Starting
from the brief hints in Dirac's book, I started to
develop the subject using class operators. This
involved me in formulating and proving many
theorems for the first time. The result, I believe, is
a class algebra approach still not found elsewhere.
I enlarged this discussion of finite groups by
bringSing in sections of my Cambridge thesis on the
groups of polymers. This is another topic rarely
mentioned. My account of spherical symmetry is
less original but aims to bring together several
different aspects of the subject. The book has had a
reasonable life and was translated into Hungarian.
MOLECULAR SOLID-STATE PHYSICS,
SPRINGER 1991
The Division of Molecular Engineering was set
up with the intention of furthering the
development of this subject into a new discipline. For this
purpose we designed new courses which brought
together the many varied aspects of the subject.
Thus, experimental work on ceramics, the design
of miniature batteries, the structure of
high-temperature superconductors were all combined with
related theoretical courses. As a contribution to
this defining of a new subject, I wrote a book,
based on my lectures on molecular solid-state
physics which tried to introduce, to chemists,
enough solid-state theory to understand the
variety of interesting new materials. The book has
been a failure, perhaps because the subject is, as
yet, very unfamiliar.
G.G. Hall's Publications in Quantum Chemistry
1.
The molecular orbital theory of chemical valency.
III. Properties of molecular orbitals.
Proc. Roy. Soc., 1950, A 202, 155.
(with Sir John Lennard-Jones).
2.
The molecular orbital theory of chemical valency.
VI. Properties of equivalent orbitals.
Proc. Roy. Soc., 1950, A 202, 336.
3.
The molecular orbital theory of chemical valency.
VII. Molecular structure in terms of equivalent
orbitals.
Proc. Roy. Soc. 1951, A 205, 357.
(with Sir John Lennard-Jones).
4.
The molecular orbital theory of chemical valency.
VIII. A method of calculating ionization potentials.
Proc. Roy. Soc., 1951, A 205, 541.
5.
The molecular orbital theory of chemical valency.
X. A method of calculating the ionization potentials
of conjugated molecules.
Proc. Roy. Soc. 1952, A 213, 102.
6.
The molecular orbital theory of chemical valency.
XI. Bond energies, resonance energies and the triplet
state energies.
Proc. Roy. Soc. 1952, A 213, 13.
7.
A survey of the principles determining the structure and
properties of molecules.
Part II. The ionization potentials and resonance energies
of hydrocarbons.
Faraday Soc. Discussion, 1951, 10, 18.
(with Sir John Lennard-Jones).
8.
The ionization of paraffin molecules.
Trans. Faraday Soc. 1952, 48, 581.
(with Sir John Lennard-Jones).
9.
The electronic structure of diamond.
Phil. Mag. 1952, 7, 43.
10.
The electronic structure of diamond.
Phys. Rev. 1952, 90, 317.
11.
Calculations on the ionization potentials of some
substituted ethylenes.
Trans. Faraday Soc. 1953, 49, 113.
12.
The electronic structure of some body-centered cubic
metals.
Proc. Phys. Soc. 1953, A 66, 1162.
13.
The ionization potentials of some paraffinic molecules.
Trans. Faraday Soc. 1954, 50, 319; 450
14.
The electronic structure of transbutadiene
calculated by the standard excited state method.
Trans. Faraday Soc. 1954, 50, 773.
15.
The molecular orbital theory of chemical valency.
(Sir John Lennard-Jones Memorial Lecture).
Sv. Kem. Tidskr. 1955, 67, 1162.
16.
The bond orders of alternant hydrocarbon molecules.
Proc. Roy. Soc. 1955, A 229, 251.
17.
The form of the effective electronic potential in
a crystal.
Proc. Phys. Soc. 1956, 8, 69.
18.
The bond orders of some conjugated hydrocarbon molecules.
Trans. Faraday Soc. 1957, 53, 573.
19.
The electronic structure of diamond, silicon
and germanium.
Phil. Mag. 1958, 29, 429.
20.
Applications of quantum mechanics in theoretical
chemistry.
Rep. Prog. Phys. 1959, 22, 1.
21.
Chemistry and quantum chemistry.
Nature 1959, 183, 158.
22.
Atomic units.
Nature 1959, 184, 1559.
(with H. Shull).
23.
Improved atomic wavefunctions using a functional
transformation.
Proc. Phys. Soc. 1960, 75, 575.
24.
Ambiguity in the determination of self-consistent
bond orders.
J. Chem. Phys. 1960, 33, 953.
25.
The stability of a wavefunction under a perturbation.
Phil. Mag. 1961, 6, 249.
26.
Ground state properties of some heterocycic molecules.
Mol. Phys. 1961, 4, 25.
(with A. T. Amos).
27.
The accuracy of atomic wave functions and
their scale, I .
Mol. Spect. 1961, 7, 410.
(with A. Fröman).
28.
Single determinant wave functions.
Proc. Roy. Soc. 1961, A 263, 483.
(with A. T. Amos).
29.
Energies of some isoelectronic series of ions.
Proc. Phys. Soc. 1962, 79, 444.
(with D. Rees).
30.
Quantum mechanical interpretation of the chemical shift
in aromatic molecules.
Tetrahedron 1962, 19, 101.
(with A. Hardisson and L. Jackman).
31.
Scaling of the Platt electrostatic model of
diatomic hydrides.
Mol. Phys. 1962, 5, 279.
(with D. Rees).
32.
Ring currents and their effects in aromatic molecules.
Proc. Roy. Soc. 1962, A 268, 328.
(with A. Hardisson).
33.
The coupling between electromagnetic waves and
excitation waves in a molecular crystal.
Proc. Roy. Soc. 1962, A 270, 285.
34.
Theory of the chemical shift in aromatic heterocycles.
Disc. Faraday Soc. 1962, 34, 15.
(with A. Hardisson and L. M. Jackman).
35.
Statistical theory of the error in approximate
wavefunctions.
J. Chem. Phys. 1963, 38, 1104.
36.
Isoelectronic sequences of hydride molecules.
Theor. Chim. Acta 1963, 1, 448.
(with D. Rees).
37.
Anisotropy of the g-factor in aromatic molecules.
Nature 1963, 198, 283.
(with A. Hardisson).
38.
Anisotropy of the g-factor in polycycic hydrocarbons.
Proc. Roy. Soc. 1964, A 278, 129.
(with A. Hardisson).
39.
The theoretical treatment of ionized molecules.
Bull. Soc. Chim. Belges 1964, 73, 5.
40.
Accuracy of calculated atomic and molecular properties.
Adv. Quant. Chem. 1964, 1, 241.
41.
Molecular orbital theory of the spin properties
of conjugated molecules.
Adv. Atom. Mol. Phys. 1965, 1, 1.
(with A. T. Amos).
42.
The direct calculation of the first-order density matrix
for atoms.
Proc. Roy. Soc. 1965, A 283, 194.
(with D. Rees and L. L. Jones).
43.
The electronic structure of ionized molecules.
III Field ionization.
Mol. Phys. 1965, 9, 29.
(with J. C. Lorquet).
44.
Relativistic effects in aromatic molecules.
Theor. Chim. Acta 1966, 4, 250.
(with R. E. Christoffersort).
45.
Kinetics of unimolecular breakdown.
J. Chem. Phys. 1966, 44, 1567.
(with R. D. Levine).
46.
Self-consistent perturbation theory for
conjugated molecules I .
Theor. Chim. Acta 1966, 5, 148.
(with A. T. Amos).
47.
Self-consistent perturbation theory for
conjugated molecules II .
Theor. Chim. Acta 1966, 6, 159.
(with A. T. Amos).
48.
The size of an exciton in a molecular crystal.
in: Quantum Theory of Atoms, Molecules and Solid State,
P.O. Löwdin, Ed.; Academic: New York, 1967.
49.
Theoretical diamagnetic susceptibilities for the Be
isoelectronic sequence.
Chem. Phys. Lett. 1967, 1, 353.
(with A. Hardisson).
50.
A variation principle for discontinuous wavefunctions.
Chem. Phys. Lett. 1967, 1, 495.
51.
A new theory of ionization potentials.
Adv. Mass. Spect. 1968, 4, 547.
52.
The physics-chemistry interaction.
Phys. Bull. 1968, 19, 297.
53.
Electronic spectra of large molecules.
in: Physical Chemistry; Vol. III;
Academic Press: New York, Chap. 9, 1969.
(with A. T. Amos).
54.
A minimum principle for atomic systems allowing the use
of discontinuous wave functions.
Int. J. Quant. Chem. 1969, 3, 69.
(with J. Hyslop and D. Rees).
55.
Calculations on some simple systems using a
new variation principle.
Symp. Faraday Soc. 1969, 2, 69.
56.
The effect of intra-molecular electric fields on molecular
ionization potentials.
Mol. Phys. 1969, 17, 49.
(with K. Gregson).
57.
Orbital equations for the transcorrelated wavefunction.
Chem. Phys. Lett. 1969, 4, 352.
(with C. E. Solomon).
58.
The one-particle Green’s function and the evaluation of
ioization potentials.
Int. J. Quant. Chem. 1970, 3-S, 659.
59.
The electrostatic interaction between TCQ and DNA.
Int. J. Quant. Chem. 1969, 35, 237.
(with W. Rodwell).
60.
A minimum principle for molecular systems allowing the
use of discontinuous wavefunctions.
Int. J. Quant. Chem. 1970, 4, 5.
(with J. Hyslop and D. Rees).
61.
A second-order calculation of the hyperfine splittings
in atomic hydrogen.
J. Phys. 1970, B3, 1195.
(with M. I. Gregson and D. Rees).
62.
The healing effect in the dissociation of the paraffin
hydrocarbons.
Int. Mass. Spect. Ion Phys. 1970, 4, 489.
(with R. D. Finney).
63.
Molecular modelling with spherical Gaussians.
Int. J. Quant. Chem. 1970, 4, 553.
(with B. Ford and J. C. Packer).
64.
Symmetry properties for the one and two electron
molecular integrals.
Int. J. Quant. Chem. 1971, 5, 657.
(with D. F. Brailsford).
65.
Molecular ionization and molecular theory.
(The Spiers Lecture).
Faraday Disc. 1972, 54, 7.
66.
Guage invariant Gaussian orbitals and the ab initio
calculation of diamagnetic susceptibility for molecules.
Int. J. Quant. Chem. 1973, 7, 15.
67.
Point charge models for molecular properties.
Chem. Phys. Lett. 1973, 20, 6.
68.
Point charge models for LiH, CH4 and H2O.
Theor. Chim. Acta 1973, 31, 311.
(with A. D. Tait).
69.
The growth of computational quantum chemistry from
1950 to 1971.
Chem. Soc. Rev. 1973, 2, 1.
70.
A model for the ab initio calculation of some solvent
effects.
Chem. Phys. Lett. 1974, 24, 501 and 1974, 26, 501.
(with I. Hylton and R. E. Christofferson).
71.
Ab initio calculations on large molecules using molecular
fragments.
J. Am. Chem. Soc. 1973, 95, 8526.
(with R. E. Christofferson, D. Spangler, and G. M. Maggiora).
72.
The generalized eigenvalue problem in quantum chemistry.
Comp. Phys. Comm. 1974, 8, 337.
(with B. Ford).
73.
Linear relations between molecular energies.
J. Am. Chem. Soc. 1974, 96, 7875.
(with J. H. McCreery).
74.
A theoretical study of tricycloquinazoline
carcinogenesis, I.
Theor. Bio.1975, 50, 107.
(with W. R. Rodwell).
75.
Floating s and p-type Gaussian orbitals.
Chem. Phys. Lett. 1975, 35, 437.
(with D. F. Brailsford, N. Hemming, and D. Martin).
76.
Conformation energies and electronic structure of
phenethylamine and amphetamine.
J. Theor. Bio. 1975, 53, 475.
(with C. I. Miller and G. W. Schnuelle).
77.
Charges and bond energies in the analysis of quantum
chemistry calculations.
Int. J. Quant. Chem. 1975, S-9, 279.
78.
On the development of quantum mechanical solvent effect
models: Macroscopic.
J. Am. Chem. Soc. 1976, 98, 7191.
(with J. H. McCreery and R. E. Christofferson).
79.
On the development of quantum mechanical solvent effect
models: Microscopic.
J. Am. Chem. Soc. 1976, 98, 7191.
(with J. H. McCreery and R. E. Christofferson).
80.
A new formulation of the correlation problem.
in: Quantum Science, Methods and Structure,
Calais, J-L.; et al. Eds.;
Plenum: New York, 1976.
81.
Computational methods for large molecules.
in: The New World of Quantum Chemistry,
Pullman, B.; Parr, R., Eds.;
Reidel: Dordrecht-Holland, 1976.
82.
Solvent effects on excited states.
in: Excited States in Organic Chemistry and Biochemistry,
Pullman, B.; Goldblum, N. Eds.;
Reidel: Dordrecht-Holland, 1977.
(with C. J. Miller).
83.
Infinite order perturbation theory.
Chem. Phys. Lett. 1977, 52, 26.
84.
Orthogonal trajectories of the electron density.
Int. J. Quant. Chem. 1977, 12, 623.
(with K. Collard).
85.
The factorized wave function.
Phys. Rev. 1977, A 18, 889.
(with C. J. Miller).
86.
On the eigenvalues of molecular graphs.
Mol Phys 1977, 33, 551.
87.
Approximate electron densities for atoms and molecules.
Israel J. Chem. 1980, 19, 255.
(with D. Martin).
88.
FSGO point charge models - their accuracy and extension
to higher Gaussians.
Theor. Chim. Acta 1981, 59, 281.
(with D. Martin).
89.
Eigenvalues of molecular graphs.
Bull. I M A 1981, 17, 70.
90.
Approximate electric potentials.
Theor. Chim. Acta 1983, 63, 357.
91.
Reactions in the liquid phase.
Int. J. Quant. Chem. 1988, S-17, 425.
92.
Fitting electron densities of molecules.
Int. J. Quant. Chem. 1984, 25, 881.
(with C. M. Smith).
93.
The harmonious molecule - a correlation problem with an
exact solution.
Chem. Phys. Lett. 1985, 122, 577.
94.
Atomic charges within molecules.
Adv. Atomic Mol. Phys. 1985, 20, 41.
95.
A simple model for a reaction surface.
Theor. Chim. Acta 1985, 67, 439.
96.
The exponential map and the representation of reaction
surfaces.
J. Mol. Str. (Theochem) 1985, 123, 179.
(with M. Okada).
97.
The diabatic energy surface for H3.
Proc. Indian Acad. Sci. (Chem Sd) 1986, 96, 207.
(with M. Okada).
98.
The approximation of electron densities.
Theor. Chim. Acta 1986, 69, 63.
(with C. M. Smith).
99.
The electron density of the water molecule.
Theor. Chim. Acta 1986, 69, 71.
(with C. M. Smith).
100.
Point charges and the molecular electrostatic potential.
Int. Rev. Chem. 1986, 5, 115.
101.
The molecular electrostatic potential of some simple
molecules.
Theor. Chim. Acta 1986, 69, 425.
(with K. Tsujinaga).
102.
The current bun model of simple molecules.
Theor. Chim. Acta 1986, 70, 257.
(with K. Tsujinaga).
103.
The evaluation of moments for polycydlic hydrocarbons.
Theor. Chim. Acta 1986, 70, 323.
104.
Optimal population analysis.
Int. J. Quant. Chem. 1987, 31, 685.
(with C. M. Smith).
105.
Diabatic surfaces which permute into one another.
Int. J. Quant. Chem. 1987, 31, 383.
106.
Equivalent orbital theory of polymers.
Synthetic Metals 1987, 17, 123.
107.
On the use of cavity models to describe muonium in
diamond, silicon and germanium.
Theor. Chim. Acta 1988, 74, 75.
(with T. A. Claxton).
108.
A new method of calculating the spin density of trapped
muonium in diamond.
Chem. Phys. Lett. 1988, 150, 23.
(with Y. Mizukami).
109.
C. A. Coulson and the surface energy of metals.
Int. J. Quant. Chem. 1988, 34, 301.
110.
Molecules with holes.
Theor. Chim. Acta 1988, 73, 425.
111.
The recognition of polycydic hydrocarbon radicals.
J. Math. Chem. 1988, 3, 233.
(with J. R. Dias).
112.
Theoretical studies on the ionization potential of
interacting atoms at large separations.
Theor. Chim. Acta, 1988, 74, 463.
(with Y. Mizukami).
113.
Intramolecular energy transfer in water.
Theor. Chim. Acta 1988,74, 23.
(with H. Nobutoki).
114.
Resonance and reactivity.
J. Mol. Str. (Theochem) 1988, 169, 233.
115.
Electric fields around molecules.
J. Mol. Str. (Theochem) 1988, 179, 293.
(with C. M. Smith).
116.
Enumeration of Kekulé structures by matrix methods.
Chem. Phys. Lett. 1988, 145, 168.
117.
The change in the dressed potential of a polyatomic
molecule in intense photon fields:
Simple rules based on the nuclear charge-mass ratio.
Int. J. Quant. Chem. 1989, 35, 283.
(with N. Saito).
118.
The continuing importance of electrostatics in chemistry.
(The Lennard-Jones Lecture).
J. Chem. Soc., Faraday Trans. 1989, 85(4), 251.
119.
The recognition of polyhex hydrocarbon radicals.
J. Math. Chem. 1989, 3, 233.
(with J. R. Dias).
120.
Aromaticity measured by Kekulé structures.
Int. J. Quant. Chem. 1991, 39, 605.
121.
Computational quantum chemistry — then and now.
J. Mol. Str. (Theochem) 1991, 234, 13.
122.
Eigenvalue distributions for the graphs of alternant
hydrocarbons.
J. Chem. Inf. Comp. Sci. 1992, 32, 11.
123.
Integral representation of a fundamental functional for the
study of the zero-point vibrational energy of hydrocarbons
and the total pi-energy of alternant hydrocarbons.
Int. J. Quant. Chem. 1992, 41, 613.
(with S. Arimoto).
124.
Linear dependence of total pi-electron energy of
benzenoid hydrocarbons on Kekulé
structure count.
Int. J. Quant. Chem. 1992, 41, 667.
(with I. Gutman).
125.
Effect of bay regions on the total pi-energy of benzenoid
hydrocarbons.
Polycycic Arom. Comp. 1992, 2, 275.
(with I. Gutman, S. Markovic, Z. Stankovic, and V. Radivojevic).
126.
Electrostatic water models.
Int. J. Quant. Chem. 1992, 42, 1237.
(with C. Smith).
127.
Eigenvalue distributions in alternant hydrocarbons.
J. Math. Chem. 1993, 13, 191.
128.
Bent benzene - boat or chair?
J. Chem. Soc., Perkin Trans. 1993, 2, 1491.
129.
Some solutions in the graph theory of alternant
benzenoids.
Int. J. Quant. Chem. 1993, 45, 167.
130.
Eigenvalue distributions and asymptotic lines of the
energy in alternant hydrocarbonys.
Int. J. Quant. Chem. 1993, 45, 303.
(with S. Arimoto).
131.
Intelligent Software: The OpenMol Program.
Comput. Phys. 1994, 8, 215.
(with G. H. Diercksen).
132.
Revisiting a simple regularity for benzenoid hydrocarbons.
Total pi-energy versus the number of
Kekulé structures.
Chem. Phys. Lett. 1995, 234, 21.
(with I. Gutman and S. Markovic).
133.
A discrete look at localization.
Intl. J. Quant. Chem. 1995, 53, 189.
(with D. Rees).
134.
Localized functions on a circle.
Int. J. Quant. Chem. 1995, 54, 351.
(with D. Rees).
135.
Localized planar atomic hybrids.
Int. J. Quant. Chem. 1995, 54, 361.
(with D. Rees).
136.
Generalized hybrid atomic orbitals.
Mol. Phys. 1996, 88, 1077.
(with D. Rees).
137.
Localized functions on sphere.
Intl. J. Quant. Chem. 1996, 60, 99.
(with D. Rees).
138.
Spherical hybrids.
Intl. J. Quant. Chem. 1997, 63, 197.
(with 0. Rees).
139.
Localized atomic hybrids: A general theory.
in: Conceptual Trends in Quantum Chemistry;
Kluwer: Dordrecht, 1997.
(with D. Rees).
140.
A theory of special points in two-dimensional solid-state
calculations.
Int. J. Quant. Chem. 1999, 74.
(with D. Rees)
141.
Cubature by scaling.
(with D. Rees), in preparation.
142.
Cubature over a square using alias functions
and symmetry.
(with D. Rees), in preparation.
143.
Some cubatures over the square and their accuracy.
(with D. Rees), in preparation.
Publications in Mathematics
Education, Etc.
144.
Permeation through a spherical membrane.
J. Theor. Bio. 1961, 1, 18.
145.
The application of mathematical thinking.
Inaugural Lecture, Univ. Nott. (1963).
146.
The teaching of quantum mechanics.
Tech Book Rev 1967, May 1.
(with D. Rees).
147.
An introduction to information theory.
Math. Teaching 1967, 40, 4.
148.
Introduction a la théorie de l’information.
Math. Paedagogia 1968, 33, 44.
149.
Model-building - an educational philosophy for
applied mathematics.
Int. J. Math. Ed. Sci. Tech. 1970, 1, 77.
(with B. Ford).
150.
Applied mathematics in the secondary school.
Int. J. Math. Ed. Sci. Tech. 1970, 1, 235.
(with A. R. Whitcomb).
151.
Modelling - A philosophy for applied mathematicians.
Bull. Inst. Math. Appl. 1972, 8, 226.
152.
Some theoretical considerations on the measurement of
the kinetics of hemolysis in individual red cells.
Uppsala J. Med. Sci. 1973, 78, 12.
(with N. V. B. Marsden).
153.
Information and entropy for a planar box.
Am. J. Phys. 1973, 41, 213.
(with S. B. Jones).
154.
A graphical model of a class of molecules.
Int. J. Math. Ed. Sci. Tech. 1973, 4, 233.
155.
Molecular models, in Mathematical Modelling.
J. G. Andrews and R. R. McLone, Eds.;
Butterworths: London, 1976.
156.
A plea for octal.
Int. J. Math. Ed. Sci. Tech. 1978, 9, 267.
157.
Applied mathematics.
in: Mathematical Education, C. T. Wain, Ed.;
Van Nostrand Reinhold: London, 1978.
158.
The assessment of modelling projects, Teaching and
Applying Mathematical Modelling.
J. Berry et aL, Eds. Ellis Horwood: Chichester, 1981.
159.
A bit of an oddball - but clever with it.
Guardian 1981, Aug., 4.
(with H. Burkhardt).
160.
Information and communication.
Int. J. Math. Ed. Sci. Tech. 1982, 13, 559.
161.
Motivation among mathematics undergraduates.
Int. J. Math. Ed. Sci. Tech. 1982, 13, 599.
162.
Information theory as a modelling course.
Bull. Inst. Math. Appl. 1983, 19, 183.
163.
Critical configurations of cars on motorways.
Int. J. Math. Ed. Sci. Tech. 1983, 10, 211.
164.
Interview with Dr. Hall.
Kagaku (Chemistry) 1984, 39, 244.
165.
Science in Japan and England - some first impressions.
Kagaku (Science) 1984, 54, 724.
166.
Innovation.
Kobunshi 1984, 33, 466.
167.
Art of citefaction.
Nature 1987, 325, 478.
168.
The promotion of creative research.
Kotai-Bunsuri 1987, 22, 439.
169.
Critical points in the potential of a set of
point charges.
Int. J. Math. Ed. Sci. Tech. 1988, 19, 857.
170.
Technical English - the language of Science.
Volume for 90 years of Kyoto University, Kyoto, 1988.
171.
Some reminiscences of a Japanese civil servant.
Bull. Inst. Math. Appl. 1989, 25, 162
172.
Entry to a Japanese University.
Bull. Inst. Math. Appl. 1990, 26, 36.
(with S. Arimoto and C. Smith).
173.
The Lennard-Jones paper of 1929 and the foundations of
molecular orbital theory.
Adv. Quant. Chem. 1991, 22, 1.
Read it
here.
174.
Signal flags; Can water in a boat ever make it more stable?
Mathematical modelling: source material for an
introductory course.
Oxford, 1995.
175.
Samuel Francis Boys 1911 - 1972.
Mol. Phys. 1996, 88, 309.
176.
George Green - Who?
Mathematics Today 1998, 34, 48.
177.
Parking geometry.
Math. Teaching 1974, 67, 56.
(with M. H. Hall).
178.
A catastropic model.
Math. Teaching (India) 1976, 11A, 165.
179.
Frozen ripples.
Bull. Inst. Math. Applic. 1979, 15, 207.
180.
Travelling waves.
J. Math. Mod. Teachers 1979, 2, 12.
181.
What kills?
Bull. Inst. Math. Applic. 1983, 19, 124.
182.
Lighting-up time.
Bull. Inst. Math. Applic. 1984, 20, 12.
183.
Animal frightener.
Bull. Inst. Math. Applic. 1986, 22, 91.
184.
Primes temple.
Bull. Inst. Math. Applic. 1987, 23, 60.
185.
Flashing pointer - A parable.
Bull. Inst. Math. Applic. 1987, 23, 93.
186.
Pythagoras again.
Bull. Inst. Math. Applic. 1988, 24, 58.
187.
Self-similar images.
Bull. Inst. Math. Applic. 1988, 24, 151.
188.
Mount Fuji.
Bull. Inst. Math. Applic. 1989, 25, 274.
189.
My rainbow.
Bull. Inst. Math. Applic. 1990, 26, 149.
190.
Vertex squeeze.
Bull. Inst. Math. Applic. 1991, 27, 189.
191.
Trailer pushing.
Bull. Inst. Math. Applic. 1991, 27, 55.
192.
Irrational wallpaper.
Bull. Inst. Math. Applic. 1992, 28, 55.
193.
Waterfall trap.
Bull. Inst. Math. Applic. 1992, 28, 172.
194.
Fuel consumption.
Bull. Inst. Math. Applic. 1993, 29, 8.
195.
n-Way switches.
Bull. Inst. Math. Applic. 1994, 30, 55.
196.
Heeling Yacht.
Bull. Inst. Math. Applic. 1994, 30, 137.
197.
Flying ducks.
Bull. Inst. Math. Applic. 1994, 30, 165.
198.
Stablest Beer.
Bull. Inst. Math. Applic. 1994, 31, 144.
(with M. I. Hamson).
199.
Tender trap.
Math. Today 1996, 32, 72.
200.
Page numbering.
Math. Today 1996, 32, 99.
201.
Rope twist.
Math. Today 1997, 33, 40.
202.
Touching pennies.
Math. Today 1997, 33, 39.
203.
Horizon distance.
Math. Today 1997, 33, 72.
204.
Mathematical monument.
Math. Today 1998, 34, 99.
205.
Mortgage repayment.
Math. Today, submitted.
206.
Nineteen times.
Math. Today, submitted.

Last updated : June 19, 2003 - 18:52 CET