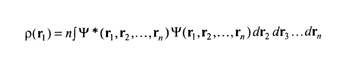The following complete article may be found under :
Peter M.W. Gill,
Obituary : Density Functional Theory (1927-1993).
Aust. J. Chem. 54, 661-662 (2001).
This article was brought to the attention
of this website by J.P. Dahl.
Obituary : Density Functional Theory
1927-1993
by
Peter M.W. Gill
University of Nottingham,
Nottingham, UK
Density Functional Theory, or DFT as she is more commonly
known, was born during 1927, in the immediate aftermath of
the Second Quantum Revolution. By the time of her death,
two-thirds of a century later, she had inspired a revolution of
her own and had launched the careers and reputations of an
entire generation of professors and conference organizers.
Although of reputable Anglo-Italian descent (1), her
legitimacy was questioned throughout her life and remains a
conversation piece in avant-garde campus cafés.
She entered an uncertain world, rocked by the revelations
of Born and Bohr and haunted by the images of half-dead
cats conjured up by her older brother, Wavefunction Theory.
He seemed able to explain almost everything - from the
mind-boggling double-slit experiment to subtle details of
molecular structure - but his wisdom often seemed to verge
on the mystical. He was particularly fond of swapping
identical particles (an annoying habit inherited from his
uncle Pauli) and drawing conclusions that baffled those with
a classical education. He called his trick 'exchange', a trivial
term for a profound phenomenon. His disturbing genius had
been recognized while he was still in his infancy and his
Nobel Prize, conferred in 1933 when he was only seven years
old, lent him a gravitas that was to dominate the relationship
with his sister for many years.
They interacted little during their childhood, and notes
from the Cambridge Philosophical Society show that, shortly
after Hartree and Fock had sketched a self-satisfied
caricature (2,3) of her brother, she was adopted (4) by her
godfather Dirac. He began to teach her how to mimic her
brother's trick but she was too young to do this properly,
except when swapping electrons within a completely
uniform density. Soon afterwards, perhaps frustrated by her
limitations, he abandoned her and, a few years before the
outbreak of war, she fell into German hands.
Von Weizsäcker rebuked her naive assumption that all
electron densities are uniform, and his insights (5) were a key
turning point in her development. However, after correcting
her concerning gradients, he too lost interest and went to
belp Heisenberg to build a bomb. Abandoned once again,
and unable to find gainful employment in Europe, she drifted
west.
Following the invention of the digital computer during the
war, there was interest in the development of computational
methods to assess the accuracy of the Hartree-Fock
caricature. Difficulties arose, primarily because Fock had
ensured that his caricature could still play the exchange
game, but Boys, Roothaan and Hall demonstrated (6-8) how
these could be overcome. However, in the same year, Slater
pointed out (9) that the task becomes very much easier if the
subtle exchange game of Wavefunction Theory is replaced
by the imitation of his sister. Admittedly, her mimicry was
imperfect in non-uniform systems, but the solid-state
physicists had convinced themselves that, in metallic
systems, the sea of electrons is calm. So, without further ado,
they declared her to be a model and embraced her.
The Xa model,
as Slater now designated her, was used
and exploited by him and others. Despite misguided attempts
to make her operate in a muffin tin, her profile quickly rose
and she became one of the first supermodels of solid-state
physics. Her successes in chemistry and molecular physics,
where her assumption of uniformity was manifestly invalid,
were less noteworthy, however.
Many young women yearn to be models, and few succeed.
Even more rarely, one has the opportunity to become a
theory. But this is what happened to our heroine when, in
1964, Hohenberg and Kohn proved that, if DFT is dressed
correctly, she can yield exactly the same information as her
complex older brother, Wavefunction Theory (10). This was an
astonishing discovery, not only because it emphasizes the
importance of proper attire, but also because it radically
altered the perceived relationship between the siblings. No
longer could he claim primacy over his sister; she had
become, in very principle, his equal.
This was such an important point that it warrants
elaboration. An n-electron system has a complex multi-
dimensional wavefunction
Y
( r 1, r 2, ... , r n)
that depends on
the coordinates of all of its electrons. From such a
wavefunction, we can obtain the familiar electron density
which gives the probability that an electron will be found at
the point r 1,
by integrating over the coordinates of all but one
of the electrons. Remarkably, according to the Hohenberg-
Kohn proof, no significant information is lost in this
integration and, therefore, the electron density is as
fundamental a variable as the original wavefunction. This
was the breakthrough that allowed Density Functional
models to aspire to the status of theories and earned Walter
Kohn a share of the 1998 Nobel Prize for chemistry.
Naturally, there was a catch and it is in the fine print. The
Hohenberg-Kohn argument is what mathematicians call an
existence proof, as opposed to a constructive proof. That is,
although we now know that, in theory, DFT can extract
as much information from r(r) as her brother can from
Y
( r 1, r 2, ... , r n)
, no-one knew how to dress her so that she
could achieve this in practice. All quantum mechanical
theories are created equal, but some are more equal than
others.
Thus she entered middle age, outwardly self-confident
but inwardly racked by self-doubt. Her admirers - and she
bad many - extolled her virtues with an evangelical fervour:
her detractors - and she had many - attacked her
shortcomings with a jealous vigour, rejoicing in her
occasional lapses and drawing unfair comparisons with her
brother's almost unerring accuracy. In truth, she was neither
as virtuous as her supporters claimed, not as flaky as the
Wavefunction aficionados alleged. She occupied an
important middle ground, neither as profligate, not as
accurate, as her brother.
But computational scientists make demanding masters
and, before long, she was being driven to change. "You
would be much more attractive", they whispered, "if you
would submit to a little parameterization. It won't hurt very
much". Not content with her elegant simplicity, they insisted
that she provide the same results as her sophisticated and
expensive brother, but at a fraction of his price. Motivated by
an insatiable hunger for perfection at no cost, they cared not
a whit for her welfare.
So the re-invention began. Layers of parameters - the
rouge of computational science - were plastered onto her
frail frame until, as the final decade of the century dawned,
she could barely recognize herself. "The panacea for all of
quantum chemistry's ills!", some declared. "Mutton dressed
as lamb", others muttered and, sickened, she silently agreed.
Finally, after suffering from a succession of excruciating
fits, she turned to an eminent Canadian surgeon. He
examined her, drew a deep breath and sighed. "There is little
that I can do for you", he admitted. "You have advanced
Hyperparametric Disorder and there is no known cure. You
should resign yourself to a future of infinite regression."
"Oh no!", she cried. "The only thing worse than rigor
mortis is the death of rigour!"
He paused. "There may be another way", he said slowly
"But it is very experimental." She looked up at him but he
turned away, unable to face her as he revealed his ghoulish
plan. "Shelley has reported (11) that it may be possible to
blend the best fragments of two beings into a single, unified
organism. The two beings are destroyed in the process, of
course, but their glorious synthesis ensures their immortality
forever! It's called half-'n'-half theory."
His proposal was now obvious. Her future lay in an
abhorrent alliance with her brother and the creation of a
grisly hybrid. The concept was as ghastly as it was
irresistible and so, in 1993, the surgeon finally released DFT
from her parametric prison (12). To the surprise of many, the
operation did not prove fatal to her brother, who continues to
flourish in a number of good universities and software
packages. Although it was soon discovered that the hybrid
had inherited Hyperparametric Disorder from its mother, it
has since attained cult status and has a huge following,
particularly among organic chemists. It has recently applied
to become a religion.
How future generations will remember pure DFT, I
cannot say. But, as we reflect on her passing and consider the
contribution that she has made to our subject, we may note
the following. She was misunderstood and abused, held in
naive awe by some and in contempt by others, capable of
stunning successes and dismal failures. Her simplicity was
seductive but her flaws ran deep and, in the end, her fall was
inevitable. But, above all, she was elegant and there is little
more that one can ask of a scientific theory.
She is survived by her older brother, her dubious offspring
and a number of poor relations, including Molecular
Mechanics, Hückel Theory, and Chemical Intuition.
References
[1] L. H. Thomas, Proc. Cambridge Philos. Soc. 23, 542 (1927);
E. Fermi, Rend. Accad. Naz. Lincei 6, 602 (1927).
[2] D. R. Hartree, Proc. Cambridge Philos. Soc. 24, 89 (1928).
[3] V. Fock, Z. Phys. 61, 126 (1930).
[4] P. A. M. Dirac, Proc. Cambridge Philos. Soc. 26, 376 (1930).
[5] C. F von Weizsäcker, Z. Phys. 96, 431, (1935).
[6] S. F. Boys, Proc. R. Soc. London, A 200, 542 (1950).
[7] C. C. J. Roothaan, Rev. Mod. Phys. 23, 69 (1951).
[8] G. G. Hall, Proc. Roy. Soc. [London], A 205, 541 (1951).
[9] J. C. Slater, Phys. Rev. 81, 385 (1951).
[10] P. Hohenberg, W. Kohn, Phys. Rev. B 136, 864 (1964).
[11] M. W. Shelley, Frankenstein, 1818. (Lackington, Hughes,
Harding, Mavor and Jones: U.K.).
[12] A. D. Becke, J. Chem. Phys. 98, 1372, (1993).
Last updated : May 19, 2002 - 20:00 CET