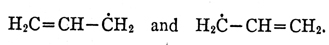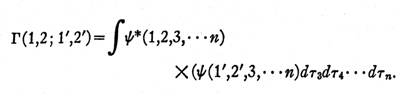We have come to the end of our conference. And
so, as we gather for our banquet, it is right
that we should thank the organizers of the conference,
particularly Bob Parr and Joop de Heer. Perhaps a
visitor from abroad may also take the opportunity, on
behalf of all the other visitors as well as himself, of
thanking our American hosts. Lastly — since this is the
first conference of this kind at which so many wives
and families have been present — an apology is now due
to all our lady friends who, having patiently put up
with our being separated from them during this last
week, must now put up with our being together and
talking yet more about our professional interests!
You have asked me to "wrap up" the conference.
This suggests some sort of parcel. Now in England there
is a limit to the length and depth of parcels permitted
by the Post Office. As for the length of this particular
parcel — I have calculated that if all the words spoken
in these 30 hours of discussion were typed in a
single row, it would just stretch from sea level to the
top of Long's Peak. Fortunately it is not all going to
be typed, though some of it is shortly to be pubiished.
And as for its depth—that is what matters most and
what I want to talk about. I do not propose to refer in
detail to any particular papers, except incidentally or
to quote what seems to me some significant bon mot.
But I believe that it would be interesting to try to
answer three questions, all of which must have been
frequently in our minds during our meetings together.
These questions are:
(1) What are the major successes of the last few
years of molecular-structure calculations?
(2) What are our own major conclusions from the
present conference?
(3) What are the lines along which it seems likely
that future progress will be achieved, and what are the
topics on which most time is likely to be spent?
You have asked me to give a personal opinion, and
I will do so. But a personal opinion will not satisfy
everyone, even though I shall try to be as fair and
objective as I possibly can when dealing with controversial
topics. Please forgive me, therefore, if you do not find
yourself in complete agreement with all that I shall say.
(1) MAJOR SUCCESSES IN THE LAST FEW YEARS
It is important to remember how old quantum
chemistry now is. It was in 1926 that Schrödinger
introduced his wave mechanics; and within two years
Heitler and London had made the first excursion into
molecular-structure calculation with its aid. The subject
is therefore just over 30 years old. It is not surprising
that many of the plums have now been picked, and
really interesting and novel fruit is harder to come by.
For before our last conference of this kind — at Texas
in 1956 — it was fair to claim that the essential nature
of the electron-pair bond was properly understood, and
so were the reasons for approximate constancy of bond
lengths and valence angles; and the difference between
localized and delocalized bonding such as that shown
by the sigma electrons in a long-chain paraffin molecule or
the pi electrons in an aromatic system like naphthalene.
We knew the reasons why resonating molecules were
especially stable, and how this resonance affected their
bond lengths. We understood the use — and limitations
— of quantum numbers to describe the electron orbitals
in a molecule, both in ground and excited states, and,
even if we could not calculate them exactly, we could
at least characterize many of the electronic transitions
revealed in ultraviolet absorption spectra. It is from
that background that we must now judge the successes
of the last few years.
In this matter I should like to point to four situations
where real progress seems to me to have been made.
There are, of course, many other places where useful
progress has been achieved. But I believe that these
are the most substantial. With the exception of the last
of the four, all these situations have been brought
before us in papers at our present conference.
The first in our understanding of what we now call
vibronic transitions. In most molecules vibrational and
electronic effects may be almost completely separated,
the coupling between the two being exceedingly small.
This is sometimes referred to as the adiabatic approximation,
in which, following the Born-Oppenheimer
approach, the function of the electronic distribution is
almost wholly to provide a potential fieid in which the
atomic nuclei may execute their vibrations. But in
certain molecules, particularly when there is a large
degree of molecular symmetry, the vibrations of the
nuclei, by destroying some of this symmetry, make
possible weak electronic transitions which would be
forbidden if, in the absence of vibration, the full
molecular symrnetry were preserved. Now electronic
and vibrational motion must be considered together.
Closely related to this are the recent exciting applications
of the Jahn-Teller theorem. This theorem,
originally published in 1937, states that if a symmetrical
nonlinear molecule has a state which is eletronically
degenerate, it will distort in such a way that the
degeneracy is removed. The magnitude of the distortion
is not provided by this discussion, nor is anything said
about the type of vibrational motion which must ensue,
particularly if the equilibrium distortions are not large.
But recently a good deal of work has been done to
estimate the distortion and to study the vibrations.
The Renner effect in NH 2 studied by Longuet-Higgins
and Pople, and the case of C 6H 6 +
studied by Moffitt
and his collaborators, are excellent examples of the
beautiful way in which theory can be used to elucidate
what might otherwise have been a peculiarly complex
situation.
The second major success of recent years has been in
the electronic spectra of aromatic radicals, where
electron-spin resonance effects have been interpreted
with great accuracy. It is an odd fact, not yet properly
understood, that there are certain situations involving
an odd number of electrons (the excited states of
ionized hydrocarbons such as naphthalene, anthracene),
where the molecular-orbital approximation appears to
work very well, even in a quite naive form; but there
are others, such as the odd-numbered neutral radicals,
where the valence-boud method is much better. It has,
of course, been known for a long time that both methods
converge to the same result, when taken to a sufficiently
sophisticated level.
Another aspect of this situation is found in the
recently discussed negative spin density. In a free
radical such as allyl H 2C—CH—CH 2,
in which there is
one unpaired electron, it is found that the unpaired
spin is most likely to be found on one or other of the
two-end carbon atoms, in accordance with the simple
resonance structures
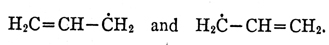
But there is a small resultant spin of opposite sign on
the central carbon atom, which may therefore be said
to have a negative spin density. This — and other
similar examples — represent a very interesting recent
success.
The third line of progress is associated with the effect
of a magnetic field. The chemical screening, as measured
in nuclear magnetic resonance studies, has given us
most important information about the distribution of
charge in a polyatomic molecule. Not all the details of
this theory have yet been adequately explored, but
there can be little doubt that in this field substantial
succcss has been achieved.
There is a fourth field that I must mention, even
if it is not represcnted at our conference. I refer to tbe
magnificent progress in the last four or five years in
converting inorganic chemistry into a discipline with a
pattern. Perhaps there have recently been too many
conferences around the topic of complex ions, coordination
compounds, and ligand-field theory. But I
cannot avoid a certain feeling of regret that nothing has
been said about these topics during this last week. It
was almost inevitable that the wider scope of
homologous series and the larger scale of molecular
architecture should have made the basic understanding of
organic chemistry easier than that of inorganic. But the
gap is closing, and in that closure the theoretician is
playing a notable part.
It may be argued that in giving this list of successes
I am being optimistic. But I recall that in one of our
sessions, when Dr. Boys was asked about the accuracy
of certain conclusions, he said that if the question were
asked after dinner he would be optimistic, but if before
dinner, he would be pessimistic. Now this address of
mine is an after-dinner speech, and I feel that I am
not being unduly optimistic in claiming that although
progress in the last five years has not been outstanding,
it has been substantial, and has materially helped in
the understanding of real chemical behavior. Naturally
enough, there have also been disappointments, and I
shall refer later to some places whcre we have had.
significant lack of success.
(2) MAJOR CONCLUSIONS FROM THIS
PRESENT CONFERENCE
Let us now turn from the major developments of the
last few years to the conclusions which have emerged
from our discussions in the last week. There is one of
these about which I feel very strongly, and because it
is of such great importance for any future conferences
on molecular structure, I make no apology for coming
straight to it. It seems to me that the whole group of
theoretical chemists is on the point of splitting into
two parts.{set bold by this website}.
Anyone who attended all the sessions this
week could be in little doubt but that the first and
second halves were quite different — almost alien to
each other. In its simplest form this difference was
associated with the large-scale use of electronic
computers, though as I shall say later, I think there is a
deeper aspect of it than just this. Now perhaps the time
has come when we ought to separate ourselves into
two or more groups, in much the same way that the one
subject of chemistry divided itself in the course of time
into organic, inorganic, physieal, and analytical chemistry.
It is the almost inevitable fate of a new subjeet,
as it grows, to split.
I mention this situation now because on three
different occasions during the last week we have heard
someone use the phrase, "Oh, but you're not doing
quantum chemistry." These occasions were:
(1) about
some of the heavy computational techniques used in
calculating energy values for atomic helium and
molecular hydrogen;
(2) about some of the calculations of
a highly empirical kind designed to estimate energy
levels and charge distributions in heteronuclear aromatic
molecules;
(3) about the tabulation and interpretation
of barriers to internal rotation in substituted ethane-
type molecules, where Bright Wilson told us (quite
wrongly, as I think!) that he wondered if he had the
right Union Card!
These three situations represent
quite distinct aspects of what we used to call quantum
chemistry. They differ considerably in their underlying
assumptions. But if each of them is now rejected by
the others as not being quantum chemistry, then the
situation is indeed serious. For my own part, I am
very far from laughing at it, and I want us to look at
it as openly and dispassionately as possible. The
questions that we are really asking concern the very
nature of quantum chemistry; what relation it has to
experiment, what function we expect it to fulfil, what
kind of question we would like it to answer.
I believe that we are deeply divided on our own
answers to these questions. It is an irony of fate that our
divisions are a logical development of recommendations
made at the I956 Texas Conference, and they show
very strikingly how easy it is to alter the balance in a
growing subject. For in I956 electronic computers were
becoming developed commercially to the stage where
it was feasible to program large computations. It was
desirable that such computers should be made available
to universities in several parts of the world. So that
conference passed a recommendation urging that more
such machines should be at the dispoal of university
departments. This recommendation was widely quoted,
and several groups (at Chicago, the Massachusetts
Institute of Technology, Cambridge, and elsewhere)
set out to exploit the new facilities by engaging in huge
programs whereby a complete molecular wave function
for a diatomic molecule (e.g., N 2 or CO) would be
calculated, including all necessary integrals, in the
space of a period measured in minutes, without any
intervention by the operator of the machine. It is in
no small measure due to the success of these programs
that quantum chemistry is in its present predicament.
There are several comments that must be made
about the two groups of quantum chemists. Thus there
is an immense amount of great computational skill and
acumen in the work of the first group. Further, there
are certain problems where it appears at present that
the only hope of settling a dispute is by computation,
since the experimental measurements are too difficult.
Examples of this sort of thing are the absorption of H -
as a function of wavelength — a matter of immense
importance in the astrophysical study of solar radiation
— and the symmetry and shape of the ground state of
the methylene radical CH 2. The first of these problems
was dealt with some years ago by Chandrasekhar; the
second has been reported by Boys at this present
conference. Obviously if work of this kind is to be effective,
it must have high accuracy; and this inevitably involves
much use of electronic computers. As a result it has
seemed to many people that this group of chemists was
so remote from the normal natural conventional
concepts of chemistry, such as bonds, orbitals, and
overlapping hybrids, as to carry the work itself out of the
sphere of real quantum chemistry.
But this matter is not simple. For at the other
extreme there are signs of great success in biology. In
the action of certain drugs it seems that the charge on
one particular nitrogen atom is of prime significance;
in carcinogenic hydrocarbons it is the electrical
properties of one (or perhaps two) parts of the molecule; in
the oxidation-reduction reactions iuvolved in
metabolism it is the basic strength or the ionization potential
or electron affinity. All these quantities can be
calculated in what we hope is at least a consistent manner
by using the grossest possible approximations, whose
crudity appears nothing less than revolting to the
"computors." Yet when the calculations are made, the
resulting correlations are too good to be treated as
simply accidental.
Where, in all this, does "real" quantum chemistry
lie? To some extent this is a matter of terminology.
But when we come to think about the possibilities of
electronic computers, It seems to me that the work
presented at our conference this week enables us to
distinguish three levels of activity. I have discussed
this matter carefully with several of the exponents of
electronic computing, and although the precise
boundaries between the three levels are not meant to be
rigid, I find that most people agree very closely with
my own division.
In the first place, if we are concerned with_molecular
or atomic systems containing 1- 6 electrons, there now
seems no reason why we should not get effectively exact
solutions. For even now we can calculate certain of
these energies as accurately as they can be measured.
Bearing in mmd the tremendous accuracy of all spectral
measurements this must be counted as a very impressive
result. As one of our members said, "The Pekeris
1078-term function for atomic helium is about as far
as it is worthwhile going." And Kolos and Roothaan
have now extended the famous James-Coolidge
calculation on H2 to include no less than 50 terms, so that
this has now become almost the best determination of
the dissociation energy of this or any other molccule.
Then, in the second place, the speeding up of calculations,
and the design of even faster machines, should
enable us to extend the range of effectivly exact
solutions. I am inclined to think that perhaps the range
6 - 20 electrons belongs to this picture. But it must be
remembered that an accuracy of this order of magnitude
will be purchased very dearly. Even in the
five-term James-Coolidge function — "the best
compromise between accuracy and simplicity" — there is
nothing easily visualized about the wave function, and
it requires a further numerical integration on an
electronic computer to derive from the full 13-term wave
function either the electronic charge density or any
other property of the molecule.
I see little chance — and even less desirability — of
dealing in this accurate manner with systems containing
more than 20 electrons. For I cannot help recalling
Hartree's remark, that if we were to print the wave
function values for the ground state of the iron atom
with sufficiently small intervals in all the electronic
coordinates, we should require a whole library to house
the books in which they were printed; and that there
are not enough atoms in the solar system to make the
paper and ink necessary to do the same thing for the
uranium atom. It looks as if somewhere around 20
electrons there is an upper limit to the size of a molecules
for which accurate calculations are ever likely to become
practicable. This range of 1 - 20 includes many
interesting questions (e.g., the dissociation of F 2, the shapes
of CH 2 and CH 3 in their ground and excited states, the
reaction H + H2 —> H2 + H and much else), but there
is a great deal that it leaves out! We are told that
above the gateway to Plato's Academy there was
written the sentence, "God is always doing Geometry."
And certainly the mathematician Jacobi said, "God
always arithmetizes." But if the range 1 - 20 electrons
were all, we could ourselves add a further statement,
"God is always computing." This is because we may
hope that eventually all problems in this range will be
solved accurately by computational techniques. Now
surely, in this way of speaking, God is computing. But
equally surely there is much more in chemistry than is
covered by this range.
I believe that the distinction between those quantum
chemists whose major interest lies in the field of 1 - 20
electrons, and consequently think in terms of full
electronic computation, and those who do not think in
these terms is so great that they deserve separate names.
During this conferenee I have thought of them as
group I (electronic computors) and group II (nonelectronic
computors), though a friend has suggested as
alternatives the ab initio-ists and the
a posteriori-ists!
I cannot help thinking that the gap between the two
groups is so large that there is now little point in
bringing them together. This is probably the last
conference of the old kind. In future we should either have
two distinct conferences, or else be prepared to plan
parallel sessions for group I and group II enthusiasts.
I have spoken of the difference between group I and
group II as if it were bound up with the use of electronic
computers. But this is an oversimplification. I have
already described group I by saying that their desire is
for complete accuracy and in order to achieve this they
are prepared to abandon all conventional chemical
concepts and simple pictorial quality in their results.
Against this the exponents of group II argue that
chemistry is an experimental subject, whose results are
built into a pattern around quite elementary concepts.
The role of quantum chemistry is to understand these
concepts and show what are the essential features in
chemical behavior. These people are anxious to be
told why, when one more vinyl group is added to a
conjugated chain, the UV absorption usually shifts to
the red; they are not concerned with calculating this
shift to the nearest angstrom; all that they want is
that it should be possible to calculate the shift
sufficiently accurately that they can be sure that they
really do possess the fundamental reason for the shift.
Or, to take another example, they want to know why
the HF bond is so strong, when the FF bond is so
weak. They are content to let spectroscopists or physical
chemists make the measurements; they expect from
the quantum mechanician that he will explain why the
difference exists. But any explanation why must be
given in terms of concepts which are regarded as
adequate er suitable. So the explanation must not be
that the eiectronic computer shows that D(H—F)
»D(F—F), since this is not an explanation at all, but
merely a confirmation of experiment. Any acceptable
explanation must be in terms of repulsions between
nonbonding electrons, dispersion forces between the
atomic cores, hybridization and ionic character. It does
not matter that in the last resort none of these concepts
can be made rigorous. For chemistry itself operates at
a particular level of depth. At that depth certain
concepts have significance and — if the word may be
allowed — reality. To go deeper than this is to be led to
physics and elaborate calculation. To go less deep is to
be in a field akin to biology. Once this is recognized it
is not difficult to see that there is a perfectly sound
basis for all three comments about "not doing quantum
chemistry" that I reported earlier.
It would be a grave disaster if quantum chemistry
were limited to either the "very deep" or the "shallow"
level of concept and operation. And certainly it would
be a serious loss if it did not maintain a close link with
experiment and with conventional thought forms of
chemistry. It is significant that in the last few years,
group II peopie like Orgel and Jörgensen have made
such excellent progress in ligand-field theory. For there
the relation with experiment, both of shape of a complex
and energy of eiectronic excitation, is immediate; yet
theory adds to what experiment can provide, each
supplementing the other.
There is always a danger — not entirely avoided this
week — that group I people will forget that chemistry
is associated with the real world. I recall an occasion
shortly after the end of the last world war, when an
exhibition of quantum chemistry was being opened in
the Palais de la Découverte in Paris. There were lovely
diagrams of the Kekulé and Dewar structures for
benzene, and excellent numerical illustrations of the
lowering in energy as more structures were allowed to
resonate among themselves. But Linus Pauling, as he
went round that exhibition and came to these diagrams,
said, "Why don't you put a bottle of the stuff by the
side of the diagrams?" It is, I believe, very important
that we should recognize this interplay of theory and
experiment. For that reason, if for no other, I was
among these who were gratified when Professor
Oosterhoff broke completely with tradition earlier today
in our last session, and actually did an experiment
before us!
I would like to carry this discussion of groups I and
II a stage further. The concepts of classical chemistry
were never completely precise, e.g., the notion of
ionic character of a bond could never be unequivocally
formulated. Thus, when we carry these concepts
over into quantum chemistry we must be prepared to
discover just the same mathematical unsatisfactoryness.
Consider as an example, the representation of the wave
function of a diatomic molecule A—B in terms of
covalent, ionic, ... functions. If we consider all states
of ionization and excitation of both A and B, we shall
have an overcomplete set of functions. This is anathema
to group I, but it is the very lifeblood of group II, who
seek for the simplest and most agreeable way of picking
out from this overcomplete set a small group of three
or four (usually not even mutually orthogonal!) which
will be "good enough" for their purpose. Mathematically,
of course, we could have dealt with the whole
problem in terms of a single atomic nucleus + electrons,
centered at either A or B. (Notice how many group I
papers have recently been discussing single-center
expansions!) But that would not be chemistry as
group II understands it. Exactly analogous situations
arise whenever, in an attempt to obtain a precise
completeness in the set of basic functions, it is found
necessary to include the continuum. It may be
mathematically desirable to do this, but — in rather
exaggerated language, which is not quite true — "who ever
heard of a chemist who bothered about the continuum?"
This leads to a further difference between groups I
and II. Many of the familiar concepts of chemistry
are associated with the separation of the total groups
of interactions between the various nuclei and their
electrons into two sections. We may call these weak
and strong interactions. Thus the idea of separate
bonds in a polyatomic molecule rests upon the conviction
that it is possible to choose certain orbitals (for
one single bond) such that the interaction between them
is strong, and yet the interaction between them and
any other orbitals is weak. But this is at best a
qualitative difference, depending on what we mean by
strong and weak. Certainly we can never get 100%
isolation of certain interactions from the rest; mathematically
therefore, a bond is an impossible concept for
group I. It is not surprising (see later) that it is
practically never used by them. Yet the existence of bond
properties is basic to all chemistry.
There are occasions where this separation into strong
and weak interactions has been exceedingly effective.
The great success of ligand-field theory (surely one of
the most typical group II projects!) seems to be bound
up with the fact that among the d electrons of a transition
element, only one basic configuration (in the atomic
sense) is needed. Ultimatcly, of course, many other
configurations should be included, and we know that
in some complexes an allowance should be made for the
delocalization of some of these d electrons away from
the central atom on to the ligands. But these may often
be treated as perturbations.
It is not surprising that the orientations of these two
groups of quantum chemists are so different that cross-
fertilization has now become much less frequent than
in earlier days.
WHAT HAVE WE FOUND OUT ABOUT ATOMS
AND SMALL MOLECULES?
I have spent a long time on the difference between
group I and group II because I believe the situation is
critical. Many members of group I do not realize what
has been happening to them; and members of both
groups display an undesirable lack of sympathy for
each other's work. But several other interesting
conclusions have emerged this week, quite independent of
any group I — group II division. Perhaps the simplest way
of referring to some of these is in the form of a numbered
list.
(1)It has become abundantly clear that until
we can cope efficiently with many-center integrals,
there will be a holdup in polyatomic molecule
calculations. As one of our conference said, "Ignorance of
4-center integrals has held up progress for 15 years" -
a comment which made me want to hurry up with a
manuscript that Michael Barnett and I have been
writing on this subject for just about 10 years! But,
alas, it is only too true that the techniques for effective
evaluation of these integrals still elude us. These are
what Mulliken and Roothaan recently called the
"bottlenecks of molecular quantum mechanics."
(2) Great accuracy has been obtained with systems
containing only 2- 3 electrons. But with slightly more
electrons (and often with the small number also) the
errors are not always clear. It would be a great help if,
when papers are being written, some guidance could be
given about the likely size of the discrepancy between
theory and experiment. Since some form of variational
method is nearly always used to calculate the energy,
it should be possible to say more about the limits of
error than is usually said. For example, even with the
prodigious calculations reported in this conference, as
soon as the number of electrons exceeds about six, the
D values for diatomic molecules are only about one-half
of the true values, and the dipole moments are
frequently 50% in error. This is a sobering conclusion, for
very large amounts of time have gone into the values
now being given to us.
(3) We need to introduce "split orbitals" (or should
we call them open-shell configurations?) if we want to
reproduce correct radial correlation of electrons in
atoms or in molecules. It has been known for a long
time that the best simple description of the ground
state of helium is not (1s) 2, where both electrons are in
the same orbital, but (1s)(1s'), where they are in
different ones. We may think of the 1s orbital as being
relatively close to the nucleus, and the 1s' orbital as
being more fully screened, and thus further away. This
situation now appears to be quite general. It is certainly
more important for inner shells than für outer ones, and
does not seriously affect the energy (configuration
interaction is far more important in lowering the
energy). In cases where there is one or more unpaired
electrons, the exchange terms between these electrons
and the inner-shell electrons leads to Hartree-Fock
equations which are different für the split orbitals, and
so adds to the splitting. We could perhaps call this an
exchange polarization. It is significant in calculations
of spin density : the Li atom with one unpaired electron
outside a split core of (1s) 2 type, and the 0 2 molecule
with two more electrons having alpha spin than beta spin, are
excellent examples.
(4) It is now perfectly clear that a single-configuration
wave function must inevitably lead to a poor energy.
This is because, among other defects, it completely
neglects correlation energy. Indications are that among
the electrons in the valence shells of atoms and molecules
this correlation energy is roughly constant per pair of
electrons. But if one electron of a pair is excited to an
outer higher-energy orbit, the correlation energy from
this pair is reduced. It is necessary, therefore, to
calculate it for each case separately. The technique that
has proved best appears to be that of including a large
number of configurations in a molecular-orbital
configuration interaction calculation. The configurations
will now be chosen so as to simplify the mathematics.
Consequently they will have little relation to some of
the older concepts which previously dominated
discussions of this kind. During this conference hardly
anyone has talked much about hybridization or bond
orbitals. It is as if almost any functions could be used,
provided only that sufficient flexibility is assured by
allowing a large enough number of linear terms. There
is a tendency, as might have been expected, to use
functions built up from atomic orbitals, and experience
seems to suggest that self-consistent-field atomic
orbitals are preferable to simple analytical ones, such as
the much-used Slater orbitals. But a penalty is exacted
from all those who use SCF atomic orbitals. Since these
functions are normally provided in the form of a table
of numerical values, the whole analysis must be carried
through on a purely numerical basis, or else we must
begin by finding some analytical expression which
adequately represents the table of values. Thanks to
the work of Löwdin and others, this is now reasonably
practicable. On the other hand, when building up
molecular orbitals by linear combination of atomic orbitals,
it hardly seems worthwhile to find the best Roothaan-
like combinations (frequently labeled as SCF molecular
orbitals, though really it is only in a restricted sense
that they are self-consistent). The advantage of the
Roothaan functions is that many of the matrix
components between the lowest energy configuration and
higher configurations vanish. But if we are to include
10 or 20 or more configurations, this simplification is
hardly worth the additional labor of first determining
SCF coefficients.
(5) A further discovery of this conference concerns
the status of Moffitt's ingenious method of "atoms in
molecules." This method arose from the recognition
that the binding energy in a molecule was only a small
fraction of the energies of the component atoms, and
should therefore be calculable by some form of
perturbation theory. The first studies of Heitler, London,
and Eisenschitz, 30 years ago, had led to a primitive
form of interaction operator. But Moffitt very considerably
extended the applicability of the idea so as to
include both neutral and ionic states of the component
atoms. Furthermore, several distinct states für each
atom, both neutral and ionized, were to be included.
Thus, to take a very simple example, in H 2 we could
say that each hydrogen atom had certain probabilities
of being in the 1s, 2s, 2p, ... state, and a certain
probability of being in the form H +, and certain other
probabilities of being in the various two-electron states
of H -. It was because of this concentration on the
individual atoms of the molecule that it received its
title "atoms in molecules." It now appears that atoms
in molecules are not really atoms in the isolated-atom
sense, so that an expansion of the molecular wave
function in terms of states of the isolated atoms does
not converge very rapidly. Thus orbital exponents
appear to differ fairly substantially, and hybridization
is different in the different parts of the molecular wave
function. As one of our conference said, "An atom isn't
an atom when it gets into a moiecule." This is a pity
because it prevents us from using experimental atomic
and ionic energies in the way that Moffitt had originally
hoped. It also implies that the idea of a valence state
is less satisfactory than we had formerly supposed. It
is not true to say that in this last week we have killed
the theory of atoms in molecules, but it is true to say
that it has been very seriously wounded.
(6) One of the most vigorously pursued lines of
research during the last few years has been the density
matrix. It has frequently been pointed out that a
conventional many-electron wave function tells us more
than we need to know. All the necessary information
required for the energy and for calculating the
properties of molecules is embodied in the first- and second-
order density matrices. These may, of course, be
obtained from the wave function by a process of
integration. But this is aesthetically unpleasing, and so
attempts have been made, by Löwdin, McWeeny, and
others, to work directly with these matrices. There is
an instinctive feeling that matters such as electron-
correlation should show up in the two-particle density
matrix. But here we are confronted by a serious lack
of success. We do know the conditions that must
be satisfied by the many-electron wave function
Psi (1,2, .. n), but we still do not know the conditions
that must be satisfied by the density matrix
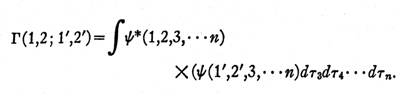
Until these conditions have been elucidated, it is going
to be very difficult to make much progress along these
lines, although some considerable insight has been
gained, particularly by McWeeny, by considering the
contributions to the density matrix that arise from
distinct and nearly separable groups of electrons.
Now clearly much else was reported during this week.
But these are some of the major conclusions. It would
be nice to be able to summarize in a simple fashion.
I doubt if it is true, as one member claimed, that a
"major break-through has occurred," but perhaps it is
true, as Lee Allen said, that "a turning point has been
reached this last summer," now that we have several
computer programs actually running. (Incidentally, the
succeSsfui development of autocoding and Fortran and
similar techniques reminds me that I shall feel that the
computer firms will not have done their job properly
until they have produced a computer that I can talk
to, and which will listen to my voice, interpret my
instructions, code itself, and then tell me the answer.
This attractive prospect — I am assured — is by no
means absurdly idealistic!) But to balance the optimism
of the "turning point" let me add a quotation from
Ruedenberg: "Diatomic molecules are peculiar because
they only have two ends, and these ends are very dose
together."
(3) FUTURE PROGRESS
We must now turn to the third question: What are
likely to be the directions of future work during the
next few years? This is a most intriguing issue, but I
believe that there have been several pointers this week,
which do at least provide clues for the future. Here again
It will be simplest to list some of these clues by number.
(1) The most important clue seems to me to be the
recognition that the energy is not the only
goodness of a wave function. In the past we have been
preoccupied with energy. This was natural enough, for
our wave equation is written in the form H Psi = E Psi and
the most powerful and widely used technique for
getting approximate solutions to this equation requires
us to concentrate almost exclusively on minimizing an
energy function. Now we have already seen that there
are great difficuities in getting even approximately exact
energies, and it has not always been clear just how rough
our associated wave functions are. The virial theorem
has been used to improve wave functions, but it has
been shown that since the introduction of almost any
variational parameter allows us to satisfy this theorem,
it is not of very great practical usefulness to us. Root-
mean-square deviations, such as the evaluation of
«H 2» - «H» 2 are difficuIt to calculate, and rather
depressing in their results.
It may perhaps be the recognition that this
preoccupation with energy was leading to steriity; or it may
be due to the developments of many types of microwave
experiments. But the fact is that attention is now
becoming concentrated much more on the smaller terms
in the Hamiltonian. These terms, usually neglected in
earlier work, include spin-spin coupling, spin-orbit
interaction, coupling of electron spin and nuclear spin,
quadrupole moments, and the influences that result
from the coupling of all these with an applied electric
and magnetic field. The most well known of all these
effects is the nuclear magnetic chemical screening, and
there are now experimental measurements for
particular molecules, which provide excellent tests for any
proposed molecular wave function. It is well known
that the ordinary diamagnetic susceptibility provides
an estimate of «r 2». But there are now experimental
measurements of many other functions of position, such
as «x 2» ,
«x / r 3» ,
« x 2 - y 2 / r 3.
These measurements are
interesting because they arise from small terms in the
Hamiltonian. These small terms are not large enough
to cause any serious modifications of the wave function
or the energy (this is why they are associated with
microwave measurements, where energy differences are
minute). But they act as measuring rods, able to be
placed within the electronic charge-cloud without
affecting it. Further, different members of this series
weight the charge cloud in different ways so that, for
example, the mean value of r 2 will tend to weight the
outer regions of the molecule, but the mean value of
x/r 3 will weight those parts of the cloud near the
particular origin being used (usually one of the nuclei). In
this way we begin to see how it may be possible to test
a given wave function for accuracy in one of several
chosen respects, rather than, as at present, in just one
aspect, its energy. Martin Karplus' survey at this
conference is surely a pointer to much future work
along similar lines.
(2) We shall be more concerned with excited states
and we must find better ways than at present for
decribing some of them. The primitive idea of one
electron being promoted to a higher orbital needs to
be supplemented by a discussion of the reorganization
among the unexcited electrons. And sometimes it is
impossible to describe an excitation in terms of a one-
electron jump. The relation between valence-shell
transitions and Rydberg-type transitions is crying out
to be explored.
(3) We shall continue to talk about correlation
energy, and its relation to the size and shape of a
molecule. I myself hope that, as at this conference, we
shall expose ourselves to those people — in this case the
theoretical physicists — who have studied the electron
theory of metals and of plasma, and shall train
ourselves to adapt some of their techniques to our own
purposes. For they have much to teach us. The UV
absorption of long conjugated carbon chains is just one
example of this.
(4) I also think that we shall consider more fully the
interactions between systems, this "omnibus" title
covers several related types of problems. On the one
hand it includes the repulsive interactions between
nonbonded atoms in the same molecule (with its
influence upon internal rotation, energy barriers, and
the possible molecular deformations due to steric
overcrowding); on the other hand, it must include
inner-shell — outer-shell forces as discussed by Pitzer and
McWeeny, and their influence on bond energies. In the
final stage it will encompass chemical reactions. It is a
sobering thought that we do not know enough about
any single reaction to be able to make a realistic
ab initio calculation of its rate. It is admittedly true
that since reactions involve the breaking and
rearranging of chemical bonds, we should try to make our
knowledge of the nonreacting molecule as complete as
we conveniently can before going on to consider
reacting ones. But much of this knowledge has been available
for several years. We ought to have been more concerned
with this at our conference, and it ought not to have
been possible for J. 0. Hirschfelder to have to say, however
jokingly, "I want to tell you all about intermolecular
forces in two minutes." Here the situation can be
summarized in three words: "Wanted, new concepts."
But I foresee that in future conferences more will be
said about this sort of thing.
(5) Finally there is the spreading of quantum chemistry
into biology. Some reference has already been made
to this. The indications here seem to be quite clear: that
more and more use will be made of wave-mechanical
ideas in this exciting field. It is already clear that the
structure of a protein chain depends very intimately on
bond distances and angles and the nature of the hydrogen
bond. But work is being initiated, by John Griffith
and others, on oxygen uptake by haemoglobin.
Professor Pullman has given a preliminary survey to this
present conference, which shows that many of the basic
and acidic properties of the amino-acid residues may
bc accounted for in exceedingly simple terms. All this
seems likely to continue, and to develop. The work
itself, however, will almost inevitably be crude, and of
the type that it is now fashionable to call semiempirical.
Group I exponents will throw up their hands in horror
at such attempts to estimate the electrostatic forces in
an energy-rich phosphate bond; even group II members
will mistrust the complete neglect of many terms and
integrals which are known to be large. But in the
establishment of correlations and primitive patterns of
understanding it does not do to be too fussy. A rough
track through the jungle precedes the construction of a
metaled highway. And there is much experience
possessed by professional biologists which could be linked
with the deeper levels of interpretation associated with
the quantum theory, to the enrichment of both. But
let no one here make his claims too easily or too
definitely. Biological systems are much more perverse than
are laboratory chemical systems. In this field the prizes
are immense — no less than the understanding and
control of life itself. The future here may be far off.
But, as was first said in rather different circumstances,
"Ce n'est que le premier pas qui coûte"; and there are
very few sensible people who would wish to deny that
in this ultimate human enterprize there is to be no
contribution from quantum chcmistry.
This surely is the place to stop, where we have
trained our eyes to seek the distant horizon. Yet perhaps,
if we may bring them back to the regions covered by
our last week's conference, three single sentences may
be permitted. This has been a most interesting and
significant conference, with many fruitful discussions
"under the counter" or "behind the scenes." For some
of us, in the words of a member of our conference,
"More good is done round a coffee table than at a
lecture bench" — which might conceivably be taken as
an argument for a coffee break in the middle of each
morning session. And, last of all, we shall probably all
of us feel that we can agree with the doyen of quantum
molecular physicists — Robert S. Mulliken — when he
said, in what ought to go down to history as one of the
most classic understatements of all time, "I believe the
chemical bond is not so simple as some people seem to
think.">