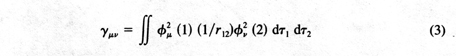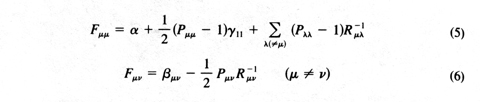John A. Pople
The following article may be found in
Int. J. Quant. Chem., 38, 349-371 (1990).
Please note: This page uses the Greek letter font type SYMBOL,
in ASCII, not in Unicode, although UTF-8 runs ok.
To view it properly you must have SYMBOL installed as a font type.
E.g. MS Windows installs this type automatically from 3.11 to XP.
| The Origin of PPP Theory |
|
 |
JOHN A. POPLE
Department of Chemistry, Carnegie Mellon University, Pittsburgh Pennsylvania 15213
Abstract
An historical account is given of the part played by the author in the development of PPP theory in the early 1950s.
The Origin of PPP - Theory
My principal contribution to PPP theory took place in the autumn of 1952. At that
time, quantum chemistry was still at a primitive stage of development. Full
computational treatments were almost entirely limited to two-electron or monatomic systems
and were carried out tediously on manual (or sometimes electric-powered)
calculators.
Some important formal developments had taken place. The
Hartree-
Fock
differential equations for molecular orbitals had been prepared and analyzed, but practical methods for their solution for polyatomic molecules were not available.
Roothaan [1]
and also Hall [2] had shown a year earlier how the Hartree-Fock problem could be
cast in algebraic form with a finite basis set, but again no implementation had been
achieved.
Boys [3] had just proposed the use of gaussian basis sets, but the idea was
initially treated with skepticism as atomic orbitals were clearly "ungaussian" in character. The electronic computer had appeared in primitive form, but its application to
electronic structure theory was still treated as a distant event.
The most active branch of quantum chemistry in the early 1950s was the semi-
empirical treatment of the p-electrons of aromatic systems, particularly hydrocarbons.
This was primarily due to the initial work of Hückel (4), who developed the independent electron model with one p-type atomic orbital per carbon atom. Neglecting
overlap integrals between different atomic orbitals, this leads to the secular equation
| Hm n - e dm n | = 0
(1)
for the energy levels in terms of the Hamiltonian matrix Hm n. Assuming the diagonal
elements Hm n to be equal to one constant a for all atoms, and taking the off-diagonal
elements Hm n to be equal to another Constant b for bonded atoms and zero otherwise,
die energy levels take the form
e = a + k b (2)
where k is a number depending only on the connectivity
of the molecule and not on
the actual values used for die parameters
a
and
b .
This separation of the structural
and parametric parts of the theory led to some elegant mathematical theorems due
to Coulson,
Longuet-Higgins,
Rushbrooke [5,6] and others. These had important
consequences, such as the separation of polycyclic conjugated system into alternant and
nonalternant classes, with significant and distinctive properties. Nevertheless, the
foundation of the Hückel theory was clearly questionable, since electrons do not interact strongly and the consequences cannot be entirely absorbed by a common
effective potential.
Some attempts had already been made to improve Hückel theory by evaluating
interaction energies between p electrons. Most notable were a 1938 paper by
Goeppert-Mayer and Sklar [7] and also the early papers of Parr and collaborators [8,9]. These
theories were of a hybrid type, in which certain integrals were treated fully (and with
considerable difficulty), while other parts were still handled by empirical potentials.
They represented a step in the right direction, but could not lead to a useful general
theory for large molecules.
In 1952, I had recently become a Research Fellow of Trinity College, Cambridge
on the basis of a thesis concerning the electronic structure of the water molecule and
its relation to liquid water. This had been supervised by Sir John Lennard-Jones (LJ)
who was Professor of Theoretical Chemistry at the time. Relieved from the pressure
of writing up this material, I was devoting a lot of time to formulating a long-term
strategy for making quantum mechanics a useful research tool in organic chemistry.
My degree was in mathematics and my qualifications as a chemist were quite tenuous.
Indeed in conversation at a College Feast, Trinity‘s distinguished organic chemist,
F. G. Mann, had challenged me with the remark: "You should not call yourself a theoretical chemist until you have discovered something about chemistry that other
chemists do not already know!" While I am sure that I defended my status, this
provoked some soul-searching and led me to pose to myself the question: "How can
quantum mechanics, as we now know it [1952], be turned into a practical procedure
which can be applied to current organic problems in the immediate future?“ This was
no doubt, an ambitious target but the formulation of difficult objectives is always a
healthy exercise in any research career.
My wife, Joy, and I were recently married and had just moved into our first home,
converted kitchen quarters of an early tudor house in the lovely Cambridgeshire village of Thriplow. I remember taking many long walks around the fields of
neighboring farms, in crisp autumn weather, thinking about future strategy. I was trying to
formulate a general approximate quantum-mechanmcal procedure which could tackle
any molecule in any conformation.
Hückel theory and its possible generalization did
not seem very attractive. In the first place, it was restricted to a particular class of
planar-conjugated molecules, whereas general molecules were usually
three-dimensional and any good structural theory would have to be able to handle this.
Secondly, Huckel theory effectively ignored the detailed effects of electron interaction, which
were large and certainly important. For example, I was impressed by the fact that
Hückel theory predicted that the ionization potential and the electron affinity of the
methyl radical should be the same, whereas a most elementary treatment including
electron interaction indicated that these two quantities should differ by the electron
repulsion of the two
p
electrons in the methyl anion, something of its order of 10 eV.
Clearly, some more realistic model was called for.
Inclusion of electron interaction seemed to require the self-consistent field
approach or its mathematical equivalent in the Roothaan-Hall equations. I was intrigued
by the possibility of applying these equations generally with a basis set of Slater-type
atomic orbitals. This would constitute a well-defined "model chemistry," leäding to a
complete set of structures, energies and force constants for all molecules. This would
now be called the HF/STO model. In 1952, of course, we had no idea whether such a
model would have a chemistry dose to "real" or "Schrödinger" chemistry. We did
not even know, for example, whether it would predict nonlinear water or tetrahedral
methane. Nevertheless, the concept of testing one level of theory against known facts and then, if successful, using the same level for predictive purposes seemed a reason-
able strategy.
Of course, full HF/STO computations were not practical at that time. There were
two major difficulties. The first was the large number of two-electron integrals required. Two centers could be handled but the smaller and more numerous three- and
four-center cases posed great difficulties. A systematic set of approximations of integrals was clearly necessary; neglect of the three- and four-center ones was the
obvious starting point. The remaining two-center integrals were commonly subdivided
into three classes: coulomb, hybrid, and exchange. The coulomb integrals
were generally the largest and the easiest to interpret physically.
g
m n
represents the interaction between electron 1 definitely assigned to the atomic
orbital
f
m
and electron 2 definitely in
f
n .
At large distances, this could be further approximated by
Rm n-1
where
Rm n
is the distance between atomic centers. So I began thinking about a theory
in which only the two-center coulomb two-electron integrals were retained; a
collection of appropriate formulae for Slater atom orbitals
f
m
was prepared.
However, even if these rather drastic integral approximations were used, there remained immense difficulties in solution of the Roothaan-Hall equations. At each
iteration of these equations, diagonalization of an N x N matrix was required, N being
the number of basis functions. Even for a molecule as small as ethane, N has the
value of 16, and repeated hand-diagonalization of such a large matrix was
unthinkable. Unlike the integral case, there seemed to be no general approximate approach to
the diagonalization problem. I approached Frank Boys and asked if he thought that
the electronic computer could help. He had been doing some preliminary experiments
on the local machine (EDSAC) but responded that diagonalization was a difficult
problem and some time would have to pass before such an application became
possible. In fact, he was unduly pessimistic, as were most people at that time concerning
tbe futWe of electronic computing. Boys himself started doing computerized diago-
nalization sometime around 1953—1954. However, I was discouraged and decided to
abandon my grand scheme, at least for the time being.
Although I was unable to handle the general three-dimensional molecule, I was
conscious that my ideas could still be applied to the more limited problem of the
pi electrons of conjugated hydrocarbons, when only one atomic orbital per carbon
atom is used. In September, Parr had published his suggestion of "zero differential overlap" [10] clearly similar to my own integral approximations. I quickly wrote
down the form of the Roothaan-Hall equations for pi electrons with these
approximations, replacing
g
m n-1
by
Rm n-1
except for the monatomic case with
m = n
With some
further changes, the new equations became
| Fm n -
e d
m n
| = 0
(4)
where
Fm n
is a Fock matrix with elements
Pm m
and
Pm n
being charge-density and bond-order quantities.
The new equations were clearly a simple generalization of Hückel theory with
minimal introduction of new parameters to allow for electron repulsion. The second
term on the right of (5) allowed for the effect of repulsion preventing the buildup
of too much electron density on a given carbon atom. The last term allowed for the
net coulomb effects of distant atoms. Both terms corrected clear physical deficiencies
of Hückel theory. I also noted very quickly that some of the important theorems
in Hückel theory still held with these new equations. In particular the Coulson-
Rushbrooke pairing theorem [5] for neutral alternant molecules was still valid with its
consequences such as uniform charge density.
The equations were more complicated than those of Hückel theory, primarily
because the Fock elements (5) and (6) depended on
Pm n
which itself depended on
the orbital coefficients. So the equations had to be solved iteratively, using the
Hückel coefficients as an initial guess. For highly symmetrical systems such as
ethylene and benzene, of course, no orbital change occurs; for other systems such
as butadiene and naphthalene, convergence was fortunately rapid. By the end of
1952, I had completed the calculations and written a draft manuscript that was close
to the paper finally published.
Early in the new year (1953), I showed the manuscript to LJ, who had been on an
extended visit to the United States while the work was being done. His initial reaction was quite negative. Although he was deeply interested in the Hartree-Fock
differential equations, LJ thought that the LCAO (linear combination of atomic orbital)
approximation to the orbitals was too poor to justify a lot of attention. His general philosophy at the time was that the differential equations should be approached
directly by some new mathematical technique such as the relaxation methods recently
developed by engineers; however, we had no detailed research along such lines. My
response was that the proposed HF/STO minimal-basis model might have serious
deficiencies, but we should find out what such deficiencies were before proceeding to
something more sophisticated. Eventually, die conversation was inconclusive. LJ did not offer to submit the paper to the Royal Society as he had done with previous
manuscripts I had presented to him; it became dormant for several weeks.
This was my first and only scientific disagreement with LJ. In hindsight, he was
correct in that a minimal LCAO basis does give a poor description of many molecules,particularly unsaturated ones. On the other hand, the LCAO approximation did later prove useful in formulating many other semiempirical theories, intermediate between
the independent-electron and full ab initio levels. Neither of us recognized the future role of electronic computers in allowing extended basis sets to be used to permit fuller flexibility in molecular orbitals. We did not discuss the topic again. At about that time, LJ announced his resignation from the Cambridge Chair and became heavily engaged in preparations for his move to the new university college at Keele, a
post that, sadly, he held only briefly before his death in 1954. I feel that, given more opportunity, I could have persuaded him to support the theory, for he always appreciated methods which led to simple physical interpretation.
Sometime in the spring of 1953 (probably March), I received an invitation to visit Charles Coulson in Oxford, where he had recently moved from King‘s College,
London. I had known him for several years, first on a visit to London when I was
still a research student and second as the external examiner of my Ph.D. thesis. With my aacceptance, I sent him a copy of my hydrocarbon manuscript. By the time I
actually went to Oxford, the first of the two major papers by Pariser and Parr [11] had
appeared in the Journal of Chemical Physics.
They had used essentially the same
integral approximations but the emphasis was on a configuration interaction and excited
states, rather than solution of the self-consistent molecular orbital equations. Coulson had read these as well as my manuscript and gave me an immediate opinion that the
two works were complementary and that mine should be published. At the time, he
was negotiating with a publisher about setting up a new journal of theoretical chemistry and asked if I would put my paper in the first issue. I agreed, but unfortunately
the journal proposal foundered. In the late summer, I received an apologetic letter
from Coulson, who then forwarded my manuscript to the Faraday Society
Transactions, where it eventually appeared in December 1953 under the title
“Electron Interaction in Unsaturated Hydrocarbons“ [12].
Bob Parr came to Cambridge to spend a sabbatical year in September 1953. We
compared notes and coordinated some notational features, but our respective
contributions were already complete — his was published and mine was in press. During
1954 and 1955, several more papers were written. Alan Brickstock, whom I was
supervising on behalf of LJ, extended the theory to radicals and ions [13]. Noel Hush
invited me to visit him in Bristol after reading my Faraday paper; this lead to a useful paper [14] on ionization potentials and electron affinities. In September 1954,
Christopher Longuet-Higgins came to Cambridge as Professor and we collaborated
on the use of the theory for excited states [15, 16]. The application to the electronic spectroscopy of radicals, such as allyl and benzyl, was particularly exciting, as experimental data was only just becoming available and needed interpretation.
It took several years for the theory to become generally accepted. I was invited to speak about it at conferences in Stockholm in March, 1955 and Austin, Texas in
Decemtber, 1955. The latter was my first visit to United States and my first exposure to the full theoretical chemistry establishment (Mulliken, Pauling, Slater, etc.). I was extrernely nervous. In 1956, Joe Hirschfelder asked me to give a similar talk at a regional American Chemical Society meeting in June in Madison, Wisconsin. This was
written up as a review and published in the Journal of Physical Chemistry [17]. This was my last PPP paper; by then my research interests had shifted to the new field of
nuclear magnetic resonance.
In retrospect, I regret some missed opportunities. In particular, the objective of a general three-dimensional theory was abandoned too soon. I eventually returned to
this after my move to Pittsburgh in 1964 and developed the CNDO (complete neglect
of differential overlap) theory with Segal and Santry. This was finally presented at the Sanibel meeting in honor of Robert Mulliken in January 1965 [18], but some-
thing similar should have been done a decade earlier. As indicated above, the general concept of such a theory existed as early as 1952 but progress was stymied by com-
putational difficulties with matrix diagonalization. Clearly, I should have pursued automatic calculation by electronic computer. Such a machine was available, albeit
unreliable and hard to use, but somehow it seemed inappropriate at that time to movea simple semiempirical theory from a sliderule (or table electromechanical calculator)
to such complicated equipment. I failed to recognize this as the true research frontier
and to press on it vigorously. Instead, I retreated to the safer and more familiar
ground of pi-electron theory.
PPP theory did achieve considerable success in the field of conjugated molecules,
particularly for electronic excited states. I think that its principal advantage was economy of complexity. The preceeding Hückel theory was clearly inadequate to treat the
excited states of even such a simple molecule as benzene. PPP theory introduced the simplest possible modifications to overcome these difficulties and thus became a
viable method for quite a wide range of molecules. As in most branches of theoretical
science, there is much merit in simplicity.
Bibliography
[1] C.C.J. Roothaan, Rev. Mod. Phys. 23, 61(1951).
[2] G.G. Hall, Proc. Roy. Soc. A205, 541 (1951).
[3] S.F. Boys, Proc. Roy. Soc. A200, 542 (1950).
[4] E. Hückel, Z. Physik 70, 204, 279 (1931).
[5] C.A. Coulson and G.S. Rushbrooke, Proc. Camb. Phyl. Soc.
36, 193 (1940).
[6] C.A. Coulson and H.C. Longuet-Higgins, Proc. Roy. Soc. A191, 39 (1947).
[7] M. Goeppert-Mayer and A. L. Sklar, J. Chem. Phys. 6, 645 (1938).
[8] R.G. Parr and R. S. Mulliken, J. Chem. Phys. 18, 1338 (1950).
[9] R.G. Parr, D.P. Craig, and I. Ross, J. Chem. Phys. 18, 1561 (1950).
[10] R.G. Parr, J. Chem. Phys. 20, 1499 (1952).
[11] R. Pariser and R.G. Parr, J. Chem. Phys. 21, 466, 767 (1953).
[12] J.A. Pople, Trans. Faraday Soc. 49, 1375 (1953).
[13] J.A. Pople and A. Bristock, Trans. Faraday Soc. 50, 901 (1954).
[14] J.A. Pople and N. S. Hush, Trans. Faraday Soc. 51, 600 (1955).
[15] J.A. Pople, Proc. Roy. Soc. A68, 81(1955).
[16] J.A. Pople and H.C. Longuet-Higgins, Proc. Roy. Soc. A68, 591 (1955).
[17] J.A. Pople, J. Phys. Chem. 61, 6 (1957).
[18] J.A. Pople, D.P. Santry and G.A. Segal, J. Chem. Phys.
43, 5129, 5136 (1965).

Last updated : Mar. 10, 2002 - 17:05