The following complete article may be found under :
C. J. Ballhausen, Quantum Mechanics
and Chemical Bonding in Inorganic Complexes.
J. Chem. Ed. 56, 357-361 (1979).
The type font "Symbol" (Greek) must be installed.
This is the third and concluding part of Carl Ballhausen's
contribution to our understanding of the "influence and
development of quantum mechanical ideas as applied to
inorganic complexes." The first part, which dealt with the static
concepts of bonding and the dynamic concepts of valency,
appeared ... {
.. here : part I .. };
the second part which initiated the
discussion of valency and inorganic metal complexes completed
in this part, appeared ... {
.. here : part II .. }
Quantum Mechanics and Chemical Bonding
in Inorganic Complexes. III.
C. J. Ballhausen
University of Copenhagen,
Copenhagen, Denmark
III. The Spread of Ideas
Valency and Inorganic Complexes (continued)
The Molecular Orbital Method
In 1935, I wrote a paper (44) outlining how crystalline potential
theory could in principle, using the Mulliken type approach, be
generalized into what is now called ligand field theory in which electrons
from the paramagnetic cation are allowed to wander onto the anions
and vice versa, so that there is incipient covalence.
These words by Van Vleck (32)
describe the fusion of the
crystal field model with molecular orbital theory. From now
on the structural unit for the wave function could be taken as
the whole complex ion, and one-electron wave functions made
up of both central and attached orbitals belonging to the same
irreducible representation can be constructed.
For the case of the octahedral group, the six ligand sigma bonds
can be combined with the 4s, 4p,
3d x 2 - y 2 and
3d z 2
metal orbitals. We have
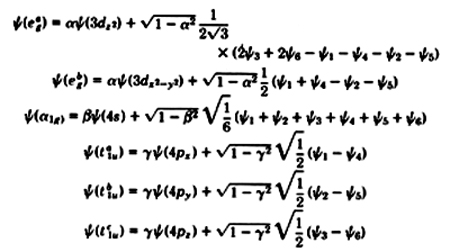
Here the s wave function of the attached
ligand i is denoted
by y i,
with ligands 1,4 located on the x axis; 2,5 on the y; and
3,6 on the z. The values of
a ,
b and
g
are determined by
solving a secular equation. The lower roots of the three
quadratic secular equations are associated with bonding levels,
while the upper roots are anti-bonding. Disregarding p
bonding, the 3d xy ,
3d xz and
3d yz
orbitals are non-bonding.
"The important term for bonding (44) is the so-called Hund
resonance integral, which is the off-diagonal matrix element
connecting the central and attached portions."
The simple Pauling theory took one electron from each
ligand and transferred it to a directed central hybrid orbital,
hf i, constructing antisymmetric
wave functions of the form
| hf i (1)
y i (2) ... |.
Notice that with a =
b =
g = SQR (1/2)
in the
molecular orbitals the number of ligand electrons associated
with the metal is given by 4·1/2 + 2·1/2 + 6·1/2 = 6, exactly as in
the valence bond method. Indeed, in this special case the
Pauling hybridized metal orbitals are connected with the
molecular orbital set by a unitary transformation, and it is
therefore immaterial which basis set is used. We have the
equation
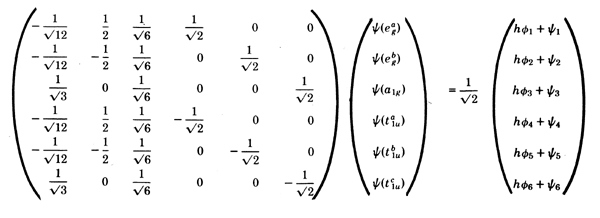
whereby hf i, i = 1, ... 6 we have
indicated the six octahedral hybrid functions.
Provided no approximations are introduced in the actual
computations, two equivalent sets of orbitals should, of course,
give the same result. However, in the valence bond method
the lack of orthogonality introduces a great many computational
complications. In the present case we notice thus that
whereas the molecular orbitals all are strictly orthogonal to
each other, y i is not orthogonal
on y j
, i ¹ j = 1,... 6. This is
the reason why so far all computations on inorganic metal
complexes have used the molecular orbital method. Actual
computations of the variational constants
a ,
b and
g
have,
however, verified Pauling's electrical neutrality principle (30).
For a complex
MX 6 +n it has been found that to a good
approximation we have
4 a 2 + 2
b 2 + 6
g 2 » n.
The 12 sigma ligand electrons in an octahedral complex are
therefore in the six bonding orbitals
a 1g, t 1u , and e g. The
"metal" electrons can then be accommodated in the
nonbonding 3d(t 2g) and the antibonding
3d(e g *).
The antibonding t 1u *
and a 1g * are higher in energy, and therefore empty.
The energy difference between
(e g *) and (t 2g) is the parameter
10 Dq which determines whether we shall have a "high spin"
complex or a "low spin" complex in the cases for which the
number of electrons n ³ 4.
In the high spin case we lose orbital
energy, but gain "exchange energy" because the electrons can
have parallel spins. In the case of the low spin we gain orbital
energy, but lose "exchange energy" because the electrons are
forced to pair-up. It is therefore a balancing of the different
energies which determines the number of unpaired spins and
not whether we have "covalent" or "ionic" bonding. Indeed,
we can pass from pure "ionic" bonding corresponding to the
crystal field model to full covalent bonding by letting
a ,
b and
g
move from 0 to SQR (1/2). We can therefore conclude that the
calculations based on the crystal field model of magnetic
susceptibilities (44)
retain practically as much significance with the molecular orbital
method as with the crystal field model, except that the size of the
crystalline potential is not to be taken too literally. The splittings of
a few volts may now relate to the magnitude of the Hund resonance
integrals rather than of the crystalline potential, but remain comparable
to the Russell-Saunders structure, making it still reasonable that
one should sometimes have the (low spin) behaviour and sometimes
the (high spin).
Apart from admiring the beauty of the paper one other
thing strikes a modern reader with amazement. Van Vleck's
paper was received by the Journal of Chemical Physics on
October 7, 1935. It was published in the December issue,
1935.
The Excited States
All considered the greatest service of the crystal field theory
derives from its ability to handle the excited states of the (3d) n
complexes. This is a unique feature of the theory - neither the
valence bond method nor the molecular orbital theory can
hope to do as well within an order of magnitude. The reasons
are, as we now know, that for many octahedral complexes of
the first transition group metals, the t 2g molecular orbitals are
to a very good approximation given by pure 3d atomic orbitals
and that the e g *
excited orbitals only are shightly contaminated
with ligand functions. In the crystal field calculations the
handling of the electron-electron repulsion terms can
therefore be taken over from the theory of atomic spectroscopy.
The first calculation of excited electronic states of an
inorganic complex was performed by Finkelstein and Van Vleck
(45) in 1940. Empirically the excited terms of the (3d) 3 system
of Cr 3+ were fairly well known. The atomic states are
characterized in a L-S scheme. Ignoring the spin-orbit coupling
the positions of all excited molecular states were evaluated for
Cr(H2O) 6 3+ using a perturbation treatment on the
complete L-S basis set.
It had long been well known (46) that the
Cr(H2O) 6 3+
complex both has a broad continuous absorption band with a
maximum at 17,500 cm -1 and some sharp lines centered at
15,000 cm -1. These bands and lines were carefully investigated
at the temperature of liquid hydrogen by Spedding and
Nutting (47) in 1934. The positions of the broad bands were
found to be very sensitive to variations in temperature, and
their edges drew in several hundred Ångströms between room
and liquid hydrogen temperature. Measurements of the
Zeeman effect in the sharp line group revealed that the
Zeeman pattern consisted of unshifted lines and of lines displaced
by +-2 b H, where
b is the Bohr magneton, H the magnetic
field.
From an analysis of the splitting pattern Van Vleck had
proven conclusively (48) that the sharp lines terminated in
an excited state having S = 1/2. The lines were therefore
"inter-system combinations," originating in the ground state
4A 2g and
terminating on 2X. In the state X the orbital momentum would
further have to be quenched either in virtue of the natural trigonal field
or the Jahn-Teller effect. As the lines are inter-system combinations,
as well as contrary to the Laporte rule, they are highly forbidden ...
They could be due to dipole transitions caused by coupling with
crystal vibrations, to magnetic dipole radiation, or quadrupole
radiation.
The tricky question of the intensity source in the crystal field
bands and lines indeed already had been treated by Van Vleck
(49) in 1937.
The presence of a spin-doublet in
Cr(H2O) 6 3+ at
15,000 cm -1
looked odd at first sight. The two lowest doublet atomic states
are 2G (15,200 cm -1) and 2P
(19,400 cm -1, actually 14,200 cm -1).
Assuming a "weak field" perturbation, that in retaining
L as a "good quantum number" the energy of the ground state
is 4A 2g(F)(-12 Dq).
For the excited doublet states we get
2T 1g(P)(0 Dq) and
2A 1g(G)(-2 Dq), 2E(G)(-2/7 Dq),
2T 1g(G)(- Dq), 2T2g(G)(13/7 Dq).
The lowest "inter-system
combination" was therefore in this scheme to be expected at
E(2A 1g - E(4A2gF) =
15,200 cm -1 + 10 Dq.
From magnetic
susceptibility measurements 10 Dq for
Cr(H2O) 6 3+ was known
to be some 15,000 cm -1. Therefore one thing stands out clearly
from the calculation that without including the effect of
matrix elements non-diagonal in L, no account can be given of
the doublet states. With full configuration interaction
included the quantum number L loses, on the other hand, all
meaning.
Taking a value of 10 Dq = 15,000 cm -1, and using a full
configurational mixing, Finkelstein and Van Vleck calculated
the lowest spin doublet state 2E g to be
18,200 cm -1 above the ground state.
The discrepancy may be due to the fact that our assumed value 1500
cm -1 of Dq ... may be a little low. There are no adequate
determinations of Dq available for chrome alum, and it in necessary for us to
base our estimates on salts not merely of different chemical
composition, but also of different valence... The doublets are brought to
within the proper distance 14,900 cm -1
of the basis quartet if we take Dq about 1820 cm -1 .
The first identification of an excited state in an inorganic
complex had been made. Finkelstein and Van Vleck must,
however, have been too accustomed to the sharp line spectra
of atomic spectroscopy to consider the claims of broad
featureless bands. The opening line of Finkelstein and Van
Vleck's paper is
Usually the spectra of solids are characterized by continuous bands
rather than discrete lines.
They then make the observation that
orbits associated with other configurations (than 3d3)
are not sufficiently
sequestered in the interior of the atom to give rise to sharp lines
.... One wonders why the line
4FA 2g - 4FT 2g has escaped
observation.
Had Finkelstein and Van Vleck identified the broad continuous
band with the maximum at 17,500 cm -1 as the looked-for
line, their calculation would immediately have given Dq =
1750 cm -1, and the first spin allowed ligand field transition
would have been identified. This had instead to wait ten
years.
Paramagnetic Rotation
Working in Göttingen with Max Born in 1928 Rosenfeld
(49) had published the quantum mechanical theory for the
natural optical activity of chiral molecules. The theory for the
rotation of the plane of polarization in a magnetic field (Faraday
effect) had likewise been treated by Rosenfeld (50) for free
paramagnetic atoms or ions. In the case of the multiplet
widths D n
small compared to kT/h and with the frequency of
the incident light being far from any absorption line, the
magnetic rotation can be expressed as a sum of two parts.
These show different dependence on frequency, and are
respectively independent of and inversely proportional to the
absolute temperature. They are referred to as the "diamagnetic"
and the "paramagnetic" terms. The diamagnetic term
arises from the splittings produced by the magnetic field in
the absorption frequencies for right and left circularly
polarized light. The paramagnetic part arises in case the
distribution of the atoms in the ground manifold depends on
temperature through the Boltzmann factors.
The paramagnetic rotation of the crystal tysonite (a mixed
fluoride of cerium and other rare earth elements) had been
treated in 1929 by Kramers (51).
Without prior knowledge of
Bethe's paper (16),
he introduced a trigonal crystal field and
derived a formula which could account for the phenomenon.
In an extremely important paper published in 1930, Kramers
developed the general theory of the paramagnetic Faraday
effect in a crystal, and proved the so-called Kramers'
degeneracy mentioned above (52): all electronic levels in molecules
containing an odd number of electrons must remain at least
two-fold degenerate provided that no magnetic field is
present.
Upon Van Vleck's instigation and under his direction
Robert Serber (53) in 1932 worked out the Faraday effect for
molecules. The formula contained, of course, the well-known
diamagnetic A terms and the paramagnetic C terms. However,
for molecules, the diamagnetic B terms were introduced.
These have the same frequency dependence as the C terms,
and stem from the mixing of the zeroth order molecular states
by the perturbing magnetic field.
Due to lack of information on the excited states Van Vleck
and co-workers (54, 55) could only try to establish a
proportionality between the paramagnetic susceptibility and the
"paramagnetic" term in the Faraday effect. Primarily the
interest before the war was therefore centered on those ground
state splittings which were comparable to kT. The first
calculation of a magneto-optical effect in a complex had to wait
until 1965 when Stephens (56) considered the allowed
"charge-transfer" transitions found in
Fe(CN) 6 3-.
The Spread of the Ideas
Our general view of the influence and developments of
quantum mechanical ideas as applied to inorganic complexes
have now reached the years 1939-40. This seems a very
suitable point to pause for a moment and take stock of the situation.
For one thing World War II broke out and curtailed so
much scientific work. The year 1939 also marks the first issue
of L. Pauling's book: "The Nature of the Chemical Bond." It
constitutes in essence a summing up of seven papers by
Pauling, published between 1931 and 1933.
Pauling's aim was to popularize the structural aspects of
chemistry. The valence bond method and the concept of
resonance were his primary tools. To this, in the case of inorganic
complexes, came the magnetic criterion for bond type. After
the war, most of this material found its way into the general
textbooks of chemistry. The book inspired and exerted a
profound influence on a generation of chemists. The immense
success of "The Nature of the Chemical Bond" (virtually
unaltered third edition, 1960) is probably due to the fact that
to a generation untrained in the formalism of quantum
mechanics it gave easy, understandable answers to very difficult
questions.
Very few - if any - chemists seem to have taken notice of
the crystal-field molecular orbital theory developed by Van
Vleck and his collaborators. Only the physics departments at
Harvard (Van Vleck); in Leiden, Holland (Kramers); and at
the Imperial College, London (Penney), could claim activities
in the field. From Holland came some magnetic measurements
by Siegert (57) and Polder (58) considered the paramagnetic
anisotropy of some Cu 2+ salts. Penney (59) showed in 1940
that the apparent irregularities of the heats of formation of
the divalent ions of the transition group can be explained if
one corrects for the crystal field stabilization of the ground
state. But from 1942 on there was silence.
In Germany most of the senior scientists had been driven
out by the Hitler regime before the war. After the war all major
German university towns were completely bombed out and
the scientific libraries destroyed. Under these working
conditions F. E. Ilse wrote his thesis in 1946 under the direction
of H. Hartmann. The place was Frankfurt am Main.
The thesis dealt with a point-charge crystal field calculation
of octahedral (3d) 1 and (3d) 2 systems.
Shortly after having
written his thesis Ilse died, and its contents were not published
(60, 61) until 1951.
It is clear that Ilse had no access to the relevant literature.
Most of his calculations of the state energies had indeed been
done by Bethe in 1929 and by Siegert (57) in 1937. What was
new, and what made history, was his identification of the
broad band found in Ti(H2O) 6 3+
at 17,500 cm -1 as a transition
between the crystal field levels
2T g -> 2Eg. Ilse further
pointed out that the transition could only occur if a molecular
skeleton vibration of T 1u or T 2u
was simultaneously excited.
The two broad "visible" bands of
V(H2O) 6 3+ were also
identified as transitions between the crystal field split components
of the atomic ground state
(3d)2 3F viz.
3T 1g -> 3T 2g and
3T 1g -> 3A 2g
3A2g. We know now that the assignment of the second band
in V(H2O) 6 3+
is wrong; the correct one being
3T 1g -> 3T 1g (3P).
With these two papers the identification of the spin-allowed
crystal field bands had thus begun.
Without being aware of the papers by Ilse and Hartmann,
Orgel (62)
working in the University of Oxford also identified
the broad featureless bands of transition metal complexes with
transitions between the crystal field levels. In his 1952 paper
he uses a strong field basis set for his calculations, that is a set
quantized after the occupation numbers n and m in
(t 2g) n (e g ) m.
The well known simiiarity between the spectra of
Cr(NH3) 6 3+ and
Co(NH3) 6 3+ found in this way
its natural explanation. The possible effects of pi-bonding between the
ligands and the t2g were also pointed out. Most important, for
the (3d)2 configuration Orgel drew a correlation diagram
which quantitatively showed how the crystal field energy
levels behaved as a function of the crystal field strength, 10
Dq.
Orgel further indicates that the unusual stereochemistry
of Cu2+ with four planar and two more distant neighbors may
be connected with the Jahn-Teller effect, as calculated by Van
Vleck (43). The effect on the heats of hydration of the crystal
field stabilization, first discussed by Penney (59), was also
rediscovered. All of these themes were to be worked over again
many times by subsequent workers.
In Japan, M. Kotani (63) had in 1949 calculated the
magnetic moments of complex ions having the electronic configurations
(t2g) n,
1 £ n £ 5.
The effective number of Bohr
magnetons were expressed in closed form using only the
parameter x = A/kT, where A is the one electron spin-orbit
coupilng parameter. Now in 1954, inspired by the work of Ilse
and Hartmann, but unaware of the paper by
Orgel (62), Y.
Tanabe and S. Sugano (64) published the complete matrices
to calculate all energy levels for the (d) n ‚
1 £ n £ 9 ,
octahedral
complexes. They also depicted all the full correlation
diagrams. Their calculation was made using the strong field
basis sets, without including the spin-orbit coupling.
In the beginning of the fifties, five centers were actively
engaged in crystal field research, namely the German school
in Frankfurt am Main, a Danish school in Copenhagen, the
Japanese school of Tanabe and Sugano, Orgel who published
three important papers from California Institute of Tech-
nology and a group of physicists in the Clarendon Laboratory
in Oxford working on paramagnetic resonance. Soon a sixth
group, headed by W. Moffitt at Harvard, was going to be
active.
Orgel both calculated and pictured some correlation
diagrams (65), gave a quantitative treatment of "the magnetic
criterion of the bond type" of complexes (66) and pointed out
that the breadth of the spectral bands (67) depended upon the
quantity d(DE)/d(Dq). He therefore explained
the sharp
bands as due to transitions inside the same
(t 2g) n(e g) m
electronic configuration and the broad bands to transitions in
which an electron is transferred from the t2g
shell to the eg
shell.
The English physicists were particularly interested in the
measurements and calculations of the paramagnetic resonance
in complexes. A magnetic field is applied to the paramagnetic
ions, so that the ground state undergoes a Zeeman effect. At
the same time the ions are subjected to a high-frequency
magnetic field, introducing transitions between the Zeeman
levels. The splittings are given as
gbH = h n.
The experimental
results are expressed using a spin Hamiltonian.
The idea of a spin Hamiltonian is to construct an operator
containing a polynomial in the components of the spin-operators
^S x, ^S y and ^S z, which
when operating on a molecular state
gives us the Zeeman energies. The perturbation procedure to
do this was developed by M. H. L. Pryce (68) in 1949. The
Clarendon Laboratory group now discovered that fitting the
data to the perturbation formulae it was necessary to use a
delocalized description of the electron wavefunction. In
particular Stevens (69) introduced pi bonding between the t 2g
metal- and ligand-orbitals.
The g factor is calculated using the operator
bH·(L + 2S).
It is only in centro-symmetric systems that L commutes with
the Hamiltonian. Furthermore, in a molecule L is not associated
with any particular center. Stevens now defined the orbital
reduction factor k p,p by
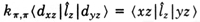 where ^lz (
where ^lz (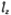 )
is the z component of the angular momentum and
|xz> is the molecular pi-orbital transforming as xz. With
f p
being the fraction of the electron which spends its time on the
ligands one can show that
k p,p =
1 - 1/2 f p ,
k p,p
is thus a measure
of the delocalization of the magnetic pi electron. The synthesis
of the magnetic features, the delocalization of the magnetic
electrons and the low lying excited "crystal field" states were
finally considered by Owen (70).
)
is the z component of the angular momentum and
|xz> is the molecular pi-orbital transforming as xz. With
f p
being the fraction of the electron which spends its time on the
ligands one can show that
k p,p =
1 - 1/2 f p ,
k p,p
is thus a measure
of the delocalization of the magnetic pi electron. The synthesis
of the magnetic features, the delocalization of the magnetic
electrons and the low lying excited "crystal field" states were
finally considered by Owen (70).
The proposal of the "sandwich" structure for bis-cyclo-
pentadienyl iron(II) in 1952 immediately produced a number
of bonding schemes. The years 1952 and 1953 saw three
qualitative electronic descriptions by E. Ruch and E. 0.
Fischer (71) in Germany and by
H. H. Jaffé (72) and Dunitz and
Orgel (73) in the U.S. The more detailed examination of the
electronic structure of ferrocene was, however, given by
Moffitt (74) in 1954. Moffitt's purpose in his paper was two-
fold:
On the other hand, it is hoped to present a plausible and useful
account of the electronic structures attributable to bis-cyclopenta-
dienyl compounds of the transition metals ... And on the other hand,
these systems are beautifully symmetrical. They therefore also offer
an opportunity to illustrate in a simple manner the principles by
means of which symmetry arguments are used to elucidate electronic
properties ... In particular, the use of group theory in the resolution
of problems with high symmetry... may be illustrated in a straight
forward fashion, and that this may aid the experimentalist in deciding
for himself the relative merits of proposed electronic structures.
Moffitt's note, and the simultaneous series of papers by
Walsh (75), marks the beginning of the impact symmetry
considerations have had on the thinking of all chemists. In the
case of ferrocene it gave a clear understanding of the essential
features of the bonding. In Moffitt's work on the optical
rotatory dispersion of transition metal complexes (76) symmetry
gave the selection rules and in the analysis of the dichroism
of certain Co3+ complexes (77) the detailed arguments rested
solely on the symmetry of the vibrational perturbations. From
that time symmetry arguments had come to stay.
It had taken the physical chemists five years (1951-56) to
assimilate the achievements of Bethe and Van Vleck. In 1956
Moffitt and Ballhausen (78) wrote a review and a bibliography
of the quantum theory of transition metal complexes which
opened the way for the full acceptance of the crystal field
theory among the inorganic-physical chemists. Moffitt died
tragically a year later, but the deed was done; the
phenomenological crystal field theory was completely explored.
{set bold by this website}
The whole field of electronic structures of
(nd)m and (nf)p
inorganic complexes was thus opened to the experimentalists.
And the inorganic chemists took to it like ducks to water.
Words like "an inorganic renaissance" were used at official
meetings and since the politicians at the same time decided
that science should be supported, money was plentiful.
{Note of this website : Coulson had a very critical position
against these on-goings -
- read more here. }. The
result was a flood of papers accumulating data in the chemical
literature. A few of them added new insight to the field; many
are justly forgotten. History therefore repeated itself in the
sixties-much the same thing had followed in the wake of
Pauling's work in the tbirties. Indeed, only a few of the
chemists who worked with inorganic complexes had had an
education in quantum chemistry. They were therefore easily
bowled over by seemingly authoritative sounding tbeories
which made sweeping generalizations and predicted trivialities.
The Molecular Calculations on Inorganic Complexes
In the crystal field model of the octahedral complexes the
quantity 10 Dq is a parameter to be adjusted in such a way as
to give the best fit to the experimental data. Attempts to
calculate this important parameter from "first principles" goes
back to the first days of crystal field theory. Bethe (16), Van
Vleck (43) and Polder (58) all tried to make estimates of 10
Dq using a simple point charge or dipole potential with
seemingly good results.
The naive crystal field model assumes that the metal
electrons are repelled by the negative charge (or dipoles) found
on the ligands. The splitting of 10 Dq of the metal d-orbitals
is then due to the orbitals' directional properties; in an
octahedron the eg orbitals point toward the ligands and the
t2g
orbitals are directed in between the ligands. Unfortunately,
when in 1952 Kleiner (79) approximated the crystal field
potential in Cr(H2O) 6 3+ by six
O 2 ions, and in order to
maintain cubic symmetry surrounded each O 2 ion by a
uniform ring charge of plus two, the calculated 10 Dq value came
out with the wrong sign. Kleiner pointed out that this result
was due to the imperfect screening of the positive nuclei in the
water molecules by the ligand electrons; the ligands attracted
the eg metal electrons instead of repelling tbem.
Already in 1935 Van Vleck had pointed out that it is the
"covalent bonding" which is the determining factor for a
calculation of 10 Dq. However, this fact was very slow in
gaining acceptance, especially among solid state physicists and
inorganic chemists. Of course, one can simulate the values of
molecular quantities by means of a point charge potential. For
instance, such a potential correctly predicts tbe cbange of sign
in 10 Dq in going from an octahedral to a tetrahedral complex
(35). Nevertheless, a point charge potential can only mimic
an infinitely more complex situation.
I believe that it was Orgel (66) who first pointed out that
by using polarized ligands to simulate the crystal field one
"neglects the Pauli principle." We may interpret this remark
as follows. In a molecular orbital calculation all orbitals come
out orthogonal to each other. Let a normalized linear
combination of ligand orbitals be called
c L. By the Schmidt
procedure we find that an orthogonalized 3d orbital has the form
c 3d - S
c L, where S is the overlap integral
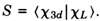 Notice now that this orthogonalization introduces a nodal
plane in the metal 3d wave function. Furthermore, the larger
S is, the larger will be the gradient at the node and
consequently the higher the kinetic energy of the "metal" electron.
With a
S(3d s) > S(3d p)
we get, therefore,
E(3d s) > E(3d p)
The dominating cause of the splitting of the d-orbitals lies
therefore in the kinetic - rather than in the potential
energy - term in the molecular Hamiltonian.
Notice now that this orthogonalization introduces a nodal
plane in the metal 3d wave function. Furthermore, the larger
S is, the larger will be the gradient at the node and
consequently the higher the kinetic energy of the "metal" electron.
With a
S(3d s) > S(3d p)
we get, therefore,
E(3d s) > E(3d p)
The dominating cause of the splitting of the d-orbitals lies
therefore in the kinetic - rather than in the potential
energy - term in the molecular Hamiltonian.
A calculation of 10 Dq for
Cr(H2O) 6 3+ using orthogonalized
orbitals were carried out by Tanabe and Sugano (80) in 1956.
The value they found was of the proper sign, but much too
large. Most importantly their work showed the necessity of
a molecular orbital approach in which the 2s and 2p ligand
orbitals are treated as valence orbitals. Ever since then, more
and more sophisticated molecular orbital calculations of 10
Dq have been carried out.
Using semi-empirical molecular orbital theory the
identification of the pi-electronic spectra of conjugated hydrocarbons
had made good progress in 1952. A natural extension of
the theory to inorganic systems was performed by Wolfsberg
and Helmholz (81) when they tried a suitably modified
semi-empirical procedure to calculate the energies of the
molecular orbitals for the ground state and the first few
excited states of the tetrahedral ions
MnO 4-,
CrO 4- and
ClO 4-.
The Wolfsberg-Helmholz molecular orbital procedure is still
with us. It has been realized that it is unsuitable for the
identification of excited states, but some scientists still believe
that molecular ground state conformations can be elucidated
using this or similar modified schemes.
We must remember that in 1952 direct attacks on problems
of electronic structures of molecules were not within the power
of electronic computers. Semi-empirical procedures, in which
one only calculated the simpler molecular matrix elements like
overlap integrals and made heavy use of experimentally
determined quantities like ionization potentials, were therefore
unavoidable. Of course, semi-empirical theories are always
open to attack from the purists. However, by using the
"Wolfsberg-Helmholz extended Hückel method" and ignoring
or compensating with "fudge factors" for the lack of rigor, light
was thrown on the electronic structures of complexes which
otherwise could not have been dealt with at the time, and
many of the results suggested new experiments of importance.
Around 1956 the basic ideas for the analytical treatment
of the electronic structures of molecules and ions had been
outlined. From then on computational science was to mint this
knowledge. What then took weeks of hard work on mechanical
desk calculators now take perhaps 30 seconds on electronic
computers. The development of the electronic computers has
indeed caused most of the computations published since 1927
when quantum chemistry began to sink into oblivion. 1956 is,
therefore, the year in which we choose to end this story.
{set bold by this website}. Our
heritage is the basic ideas, the quantitative results, and the
chemical insight gained during the last 50 years.
The Moral of the Story
The why? and how? as related to chemical bonding were in
principle answered in 1927; the details have been worked out
since that time. We can now give quantitative answers to
questions which before were answered using general phrases
like "electrovalency," "ionic," "covalent" and the like. New
incantations like "preservation of orbital symmetry,"
"electrocyclic" - the list can be augmented ad libitum - have been
substituted for the old ones. Chemistry has moved on and a
deeper understanding has been reached.
Each new generation of scientists works within a paradigm.
{set bold by this website}.
For one thing this means that the manifold of performed
experiments can be classified. However, after a shorter or longer
time the old concepts are no longer capable of accommodating
the accumulated evidence. A new, usually more abstract
paradigm must take the place of the old before significant
advances can be made again. The social and economical ideas
of our time are really hundreds of years old. But the quantum
theory is a child of the twentieth century and in many ways
its greatest achievement.
Once the theory was there, the theoretical advances have
to a large extent been coupled to the progress of instruments
and instrumentation. In the modern history of chemistry one
of the first available electronic machines was the Gouy balance
for measuring magnetic susceptibilities. It followed that
theories dealing with magnetism of complexes were developed
quite early. The conventional spectrograph was really only
good for measuring line spectra. Therefore, no broad
unstructured bands were investigated systematically before the
advent of the spectrophotometer in the late forties. The
detailed theory of the ligand field bands had, therefore, to wait
until then. The microwave technique focussed attention on
the resonance phenomena. The availability of the rotatory
dispersion instruments made the theory of optical rotatory
dispersion undergo a beautiful advance. The ESCA and the
Hea machines stimulated work on Hartree-Fock orbital
energies. And, of course, the big electronic computer pushed
and still pushes the tractable calculations to limits which were
unheard of yesterday.
Today we realize that the whole of chemistry is one huge
manifestation of quantum phenomena. Wjthout a background
in quantum theory it is impossible to possess an "in depth"
understanding of chemistry. The elucidation of chemical
phenomena by means of the quantum laws is now left to the
chemists; the solid state physicists do not have the necessary
chemical background and the high energy physicists are not
interested in electrons. Let us therefore think in deep
gratitude and admiration of those pioneering physicists who
opened the doors to modern chemistry. They are the giants
on whose shoulders theoretical chemistry is standing.
Literatur
(44) Van Vleck, J. H., J. Chem. Phys. 3, 807 (1935).
(45) Finkelstein, R., and Van Vleck,
J. H., J. Chem. Phys., 8, 790 (1940).
(46) Sauer, H., Ann. d. Physik IV Folge, 86, 197 (1928).
(47) Spedding, F. H., and Nutting, G. C., ‚
J. Chem. Phys., 2,421(1934); 3, 369 (1935).
(48) Van Vleck, J. H., J. Chem. Phys., 8, 787 (1940).
(49) Rosenfeld, L., Zeit. Physik., 52, 161 (1929).
(50) Rosenfeld, L., Zeit. Physik. 57, 835 (1930).
(51) Kramers, H. A., Proc. Acad. Amst., 32, 1176 (1929).
(52) Kramers, H. A., Proc. Acad. Amst., 33, 595 (1930).
(53) Serber, R., Phys. Rev., 41, 489 (1932).
(54) Van Vleck, J. H., and Hebb, M. H., Phys. Rev., 46, 17 (1934).
(55) Van Vleck. J. H., and Penney, W. G., Phil. Mag., 17, (1934) 961.
(56) Stephens, P. J., Inorg. Chem., 4, 1690 (1965).
(57) Siegert, A., Physica, 3, 85 (1936); 4, 138 (1937).
(58) Polder, D., Physica, 9, 709 (1942).
(59) Penney, W. G., Trans. Far. Soc., 36, 627 (1940).
(60) Ilse, F. E., and Hartmann, H.,
Zeit. für Phys. Chem., 197, 239 (1951).
(61) Ilse, F. E., and Hartmann, H., Z. Naturforschg., 6a, 751 (1951).
(62) Orgel, L. E., J. Chem. Soc., 4756 (1952).
(63) Kotani, M., J. Phys. Soc. (Japan), 4, 293 (1949).
(64) Tanabe, Y., and Sugano, S.,
J. Phys. Soc. (Japan), 9, 753 & 766 (1954).
(65) Orgel, L., J. Chem. Phys., 23, 1004 (1955).
(66) Orgel, L., J. Chem. Phys., 23, 1819 (1955).
(67) Orgel, L., J. Chem. Phys., 23, 1824 (1955).
(68) Pryce, M. H. L., Proc. Phys. Soc. (London), A63, 25 (1950).
(69) Stevens, K. W. H., Proc. Roy. Soc., A2l9, 542 (1953).
(70) Owen, J., Proc. Roy. Soc., A227, 183 (1955).
(71) Ruch, E., and Fischer, E. O., Z. Naturforsch., 7b, 676 (1952).
(72) Jaffé, H. H., J. Chem. Phys., 21, 156 (1953).
(73) Dunitz, J. D., and Orgel, L. E., Nature, 171, 121 (1953).
(74) Moffitt, W., J. Amer. Chem. Soc., 76, 3386 (1954).
(75) Walsh, A. D., J. Chem. Soc. (London), 2260 (1953).
(76) Moffitt, W., J. Chem. Phys., 25, 1189 (1956).
(77) Ballhausen, C. J., and Moffitt, W.,
J. Inorg. Nuc. Chem., 3, 178 (1956).
(78) Moffitt, W., and Ballhausen, C. J.,
Ann. Rev. Phys. Chem., 7, 107 (1956).
(79) Kleiner, W. H., J. Chem. Phys., 20, 1784 (1952).
(80) Tanabe, Y., and Sugano, S.,
J. Phys. Soc. (Japan),11, 864 (1956).
(81) Wolfsberg, M., and Helmholz, L.,
J. Chem. Phys., 20, 837 (1952).
Goto:
Quantum Mechanics
and Chemical Bonding in Inorganic Complexes. I.
Quantum Mechanics
and Chemical Bonding in Inorganic Complexes. II.
Quantum Mechanics
and Chemical Bonding in Inorganic Complexes. III. = this page here, go top
Last updated : Apr. 23, 2002 - 20:30 CET




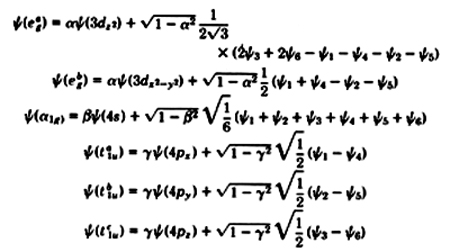
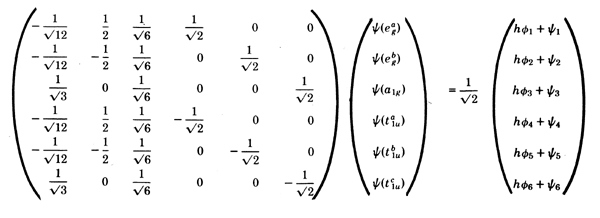
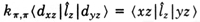 where ^lz (
where ^lz (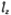 )
is the z component of the angular momentum and
|xz> is the molecular pi-orbital transforming as xz. With
f p
being the fraction of the electron which spends its time on the
ligands one can show that
k p,p =
1 - 1/2 f p ,
k p,p
is thus a measure
of the delocalization of the magnetic pi electron. The synthesis
of the magnetic features, the delocalization of the magnetic
electrons and the low lying excited "crystal field" states were
finally considered by Owen (70).
)
is the z component of the angular momentum and
|xz> is the molecular pi-orbital transforming as xz. With
f p
being the fraction of the electron which spends its time on the
ligands one can show that
k p,p =
1 - 1/2 f p ,
k p,p
is thus a measure
of the delocalization of the magnetic pi electron. The synthesis
of the magnetic features, the delocalization of the magnetic
electrons and the low lying excited "crystal field" states were
finally considered by Owen (70).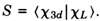 Notice now that this orthogonalization introduces a nodal
plane in the metal 3d wave function. Furthermore, the larger
S is, the larger will be the gradient at the node and
consequently the higher the kinetic energy of the "metal" electron.
With a
S(3d s) > S(3d p)
we get, therefore,
E(3d s) > E(3d p)
The dominating cause of the splitting of the d-orbitals lies
therefore in the kinetic - rather than in the potential
energy - term in the molecular Hamiltonian.
Notice now that this orthogonalization introduces a nodal
plane in the metal 3d wave function. Furthermore, the larger
S is, the larger will be the gradient at the node and
consequently the higher the kinetic energy of the "metal" electron.
With a
S(3d s) > S(3d p)
we get, therefore,
E(3d s) > E(3d p)
The dominating cause of the splitting of the d-orbitals lies
therefore in the kinetic - rather than in the potential
energy - term in the molecular Hamiltonian.